[<- Previous] [Contents of this lecture] [Next ->]
We now leave the "interfacing" steps of the action and hammer and focus our attention on the result, the vibrating string. The detection of the string motion was accomplished by utilizing the law of induction - "when a conducting wire is moving in a magnetic field a voltage is generated across the wire." For this purpose we applied a concentrated magnetic field at a desired point along the string by the use of a small, strong magnet. The induced voltage over the string - unfortunately very low due to the short-circuiting iron frame - was proportional to the string velocity at the point of the magnet.
The string motion on each side of a hammer in the middle section of the piano is illustrated in Fig. 15. On the side facing the bridge (upper panel) one sees the following.
First the initial pulse, or hump (I) passes on its way to the bridge. Then nothing happens for a period of time, while the string is at rest a little displaced relative to its equilibrium position. After some delay, corresponding to the travelling time to the bridge and back again, the pulse returns (II), now turned upside down (inverted) on reflection at the bridge. The pulse continues to the agraffe where it is reflected once more and turned right side up. Shortly after this reflection, the pulse returns to the observation point (III). (Because of the short distance between the hammer and the agraffe, the travelling time from the hammer and back again is very short, and the incoming pulse (II) and reflected pulse (III) partly merge.) The first period of the string motion is now completed, and the pulse continues towards the bridge for the next round trip, and the process repeats.
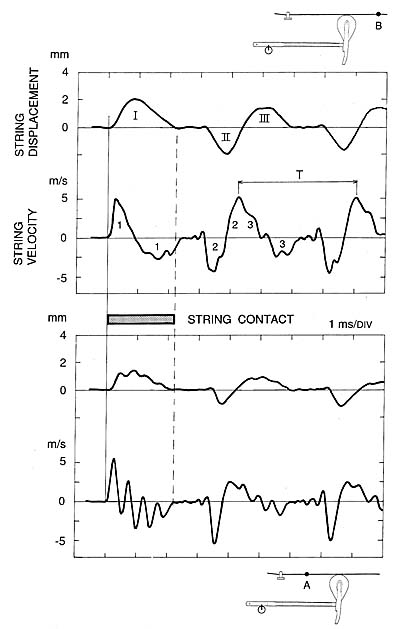Fig. 15. String motions close to the hammer; bridge side, observation point B (upper panel), and agraffe side, observation point A (lower panel) fro a C4 note atfortelevel.In the displacement curve (I) denotes the initial outgoing pulse, (II) the same pulse after the first reflection (at the bridge), and (III) the same pulse after the second reflection (at the agraffe). The corresponding pulses in the velocity curve are denoted by 1, 2 and 3. Note that each passing displacement pulse corresponds to a positive velocity wave (up) as well as a negative (down). The round-trip time for a pulse on the string (period time) is indicated by T. Observe that the string motion on the agraffe side is entirely different from the motion on the bridge side during the hammer-string contact.
The curve displaying the string velocity may be somewhat more difficult to interpret, but is in fact more informative on the very details of the process. A hump passing the magnet, which is observed as a single pulse in the displacement curve, corresponds to a positive and a negative peak in the velocity curve. This is so since the string moves in the opposite direction during the latter half of hump when the string is restored to its initial position. Remember also that the velocity is high where the slope of the displacement curve is steep.
On the other side of the hammer, towards the agraffe (Fig. 15, lower panel), the picture is entirely different during the initial moment when the hammer is still in contact with the string. During that period, the hammer acts as a temporary string termination and the initial pulse is reflected back and forth on the short string segment between the hammer and the agraffe. This causes repeated impulses on the hammer, and after about four or five such impulses the hammer is released from the string. In fact, this motion of the trapped pulse on the short string segment is the major mechanism of hammer release for most notes on the piano.
[< Previous] [Top] [Contents of this lecture] [Next >]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music