 Fig. 11. Striking ratio (d/L) for two contemporary pianos and for 1720 Cristofori.
Fig. 11. Striking ratio (d/L) for two contemporary pianos and for 1720 Cristofori.

[<- Previous] [Contents of this lecture] [Next ->]
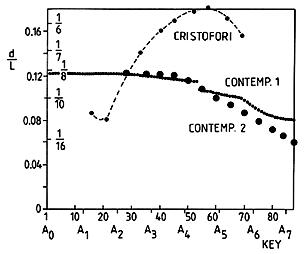
The hammer striking ratio (d/L) for the 1720 Cristofori piano and for two representative modern pianos is shown in Fig. 11. Here L stands for the speaking length of the string and d is the distance from the closest string support (the agraffe) to the point where the hammer strikes. The values for the 1720 piano seem to wander over a wide range to no apparent purpose. Early makers did not fully appreciate the effect of varying d/L but by the late 18th century, piano makers began to know what values work best (Harding 1933). Many books about pianos state that the best place for the hammer to strike the strings is between 1/7 and 1/9 of their speaking length. (Good 1982, Marcuse 1975, Mc Ferrin 1972, Briggs 1951, White 1946, Wood 1944, Vant 1927, Ortman 1925, Wolfenden 1916, White 1906, Hansing 1888, Brinsmead 1879, Helmholtz 1863).
 Fig. 11. Striking ratio (d/L) for two contemporary pianos and for 1720 Cristofori.
Fig. 11. Striking ratio (d/L) for two contemporary pianos and for 1720 Cristofori.
This is certainly not true for all the notes of modern pianos. In the best modern grand pianos the smallest treble hammer (C8) is always positioned at the factory for each piano individually and is set to produce the loudest tone. This normally occurs for a d/L-value much smaller than 1/9, usually in the range between 1/12 and 1/17. As you can see from the curves labeled "contemporary" in Fig. 11, d/L in the bass is a little less than 1/8, and it decreases gradually up to around A4 (note 49), and then decreases rapidly. How d/L should vary across the compass depends on a number of factors and is decided by the designer of the piano.
In the mid-treble, the best striking ratio often is a compromise between maximum first partial energy and the most graceful tone. Reducing the striking distance in this region generally makes the tone sound thinner because less fundamental energy is present. Increasing the striking distance makes the tone fatter, but may produce an unclear, muddy quality. Here, hammer weight is also an important factor.
In the lower part of the scale, hammer contact time is small in comparison with the roundtrip time for the pulse on the string - from the striking point to the bridge and back again. Consequently, damping due to the hammers is small. Moving the striking points of the hammers changes the tone quality primarily by rearranging the relative amplitude of the partials. If the hammer should strike the string at a nodal point, or near, where the string motion is small, then the amplitude of the corresponding partial will also be small.
Fig. 12 shows how the measured output of one particular string varied as the hammer striking ratio was changed. The graph shows partials 5 through 9. The amplitude of each partial passes through a distinct minimum point as the striking ratio is increased. If you were listening to the tone of the string you would hear obvious differences in timbre as the hammer striking distance was changed, and I am sure you would like the tone at certain d/L-values better than at others.
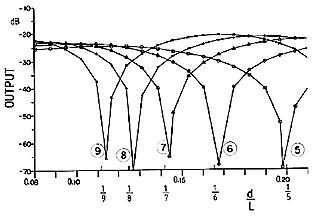 Fig. 12 Output vs. striking ratio (d/L) for partials 5, 6, 7, 8, and 9.
Fig. 12 Output vs. striking ratio (d/L) for partials 5, 6, 7, 8, and 9.
Fig. 13 shows the instantaneous peak output spectrum for two different values of the hammer striking ratio. For d/L = 0.019 (1/53), the lower partials all have very small amplitude. This is because the hammer is striking almost at the very end of the string. For such a small d/L the tone sounds thin and weak. For a longer striking distance, d/L = 0.143 (1/7), the lower partials have gained in amplitude and the 7th partial is almost completely missing. At one time it was believed that the 7th and 9th partials were dissonant and ought to be eliminated by a proper choice of the striking distance. Personally, I do not believe that any string partial should be deliberately minimized.
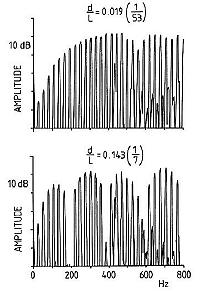 Fig. 13. String spectra for short and long striking ratio (d/L = 0.019 and 0.143).
Fig. 13. String spectra for short and long striking ratio (d/L = 0.019 and 0.143).
[<- Previous] [Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music