[<- Previous] [Contents of this lecture] [Next ->]
Before investing all our future efforts in the exact behavior of the hammers, it would be good to remind ourselves whether there are other effects not represented in our ideal theory which would also need to be taken into account. Fig. 21 (from Hall & Askenfelt 1988) tries to summarize several possibilities. One we can easily dispose of is the fact that the hammer contact is spread over as much as 5 or 10 mm of string rather than being concentrated at a single point. This is still such a small fraction of the string length that it should not matter except for frequencies above the line at the upper left - but these are so high that their strength in piano spectra is of no importance anyway.
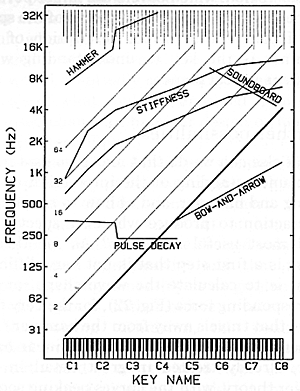Fig. 21. Estimates of frequencies above which hammer width, string stiffness, and soundboard motion become important in determining string spectra. (The "pulse decay" line indicates an upper limit for trusting the picture of Fig. 4, and "bow-and-arrow" a lower limit for trusting Fig. 3.)
Another problem with the simple theory is that it assumes both ends of the string are mounted on perfectly rigid supports, yet we know that the bridge actually moves. This means that some energy is lost from the string to the soundboard, so that the reflected waves are not really quite as strong as the theory supposed. This in turn changes the force that the hammer will provide later when it is interacting with those waves. I have estimated that this should be taken into account for the last octave or two at the treble end (above the line "soundboard" in Fig. 21), where it will help explain why those spectra are very steep; but otherwise it may be of only minor importance.
A third effect which is more generally important comes from the finite thickness of the strings. Where it works quite well to talk of harpsichord strings as if they are perfectly flexible, piano strings are much thicker and resist bending. This stiffness, I should point out, is not a nonlinear effect; it is merely something which aids the applied tension in trying to make the string straight. I have estimated in two different ways when this might become important, shown by the two lines "stiffness" in the upper part of Fig. 21. Above these lines, the predicted spectra should really be a little steeper, as the stiffness makes it more difficult to set those high-frequency vibration modes into motion. But in the central part of this figure is a region, including something like the first ten harmonics of middle˙C, for instance, where none of these other details should be very important. In this region, which covers the larger portion of the strong and interesting parts of the spectra, I believe the correct description of the hammer is the key to understanding what happens in real pianos.
[<- Previous] [Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music