Back to Contents of Five lectures...
The scientific study of the acoustics of the piano goes back to Hermann von Helmholtz (1821 - 1894), a German physician and scientist, active in both neurology, optics, electricity and acoustics. He compiled much of his thinking about sound, musical instruments and hearing in a book "On the Sensations of Tone", which still is very much worth reading.(*) Helmholtz's interest in musical instruments was strongly coupled to the perception of their sound. In view of his limited measurement equipment - in which his ears played a central role - he made remarkable contributions to the understanding of the tonal characteristics of several musical instruments, among them the piano. In a series of Appendices, of which some have become more famous than the text itself, he also presented theoretical analyses, including the case of a string struck by a hammer.
Helmholtz was followed by occasional studies during the decades around the turn of the century. These early investigators dealt in particular with the interaction between the hammer and the string, a question which in fact still not has been completely settled. After important pioneering works on almost every aspect of the piano in the 40's and 50's, by the use of what we would call rather modern equipment, the study of the acoustics of the piano has gained a renewed interest during the last decade. Although many, many questions remain to be answered, a deeper understanding of the sound generation in the piano now seems less remote than for several other instruments, in particular the bowed instruments.
The piano was invented in the 18th century, developed to its present design during the 19th century - a period during which the bulk of classical piano music was written - and produced on a large scale and frequently used in all kinds of music during the 20th century. However, a complete understanding of the acoustics of the instrument will probably not be reached until the next century. This may sound a little discouraging from a scientific point of view, but the same statement holds true for almost all traditional instruments. The situation is nothing but a result of man's incredible ingenuity in developing sound sources which not only produce a pleasant sound, but which can also be intimately controlled by the player. This evolution has resulted in musical instruments for which the acoustical function turns out to be extremely complex, despite the fact that the instruments are based on seemingly simple principles and made of common materials.
The piano is a representative example among the string instruments. The principle of its function is indeed simple; a felt hammer strikes a metal string which is connected to a large wooden plate. The string is set in vibration by the impact, and the vibrations are transferred to the plate which radiates the sound. However, for none of the steps in this process - the collision of the hammer with the string, the transmission of the string vibrations to the wooden plate, and the radiation of sound from the plate into the air - the physics is well enough understood to permit a detailed description of what actually happens in the real instrument. In addition, "simple" materials like felt and wood turn out to have very complex properties - different from sample to sample! -which further increases the difficulty of describing the phenomena.
All this would have been enough, but the most cumbersome step is yet to come. The quality of a traditional instrument is rated using our hearing as the ultimate test instrument. This means that results of acoustical measurements should always be viewed in the light of how they relate to the perceived sound. But this may not even be possible, because the perception of sound, especially musical sounds, is a field which unfortunately is very poorly explored. There are still many gaps in our knowledge of the relationship between physical and perceptual properties of sounds. For this reason, many interpretations of experimental results must remain on the level of advanced guesses.
With these difficulties in mind it is not surprising that it was possible to put a man on the moon before the acoustics of a traditional instrument like the piano had been thoroughly explained.
In contrast to most other traditional instruments like the violin or the trumpet, whose origins vanish in the haze of the past, a specific year and name can be attributed to birth of the piano. In 1709 the Italian harpsichord maker Bartolomeo Cristofori replaced the plucking pegs in a harpsichord by small leather hammers which he let strike the strings. Since this new design allowed the notes to be played either soft or loud depending on how the key was struck(**), he called his new instrument gravicembalo col piano e forte ("a large harpsichord with soft and loud"). Soon the grandiose name was shortened to pianoforte or fortepiano and eventually to piano.
Cristofori's piano was developed from the harpsichord and consequently rather small and made entirely out of wood. As time passed, however, the development of larger instruments with more and heavier strings at higher tensions - all in order to increase the volume of sound - necessitated a more rigid construction. The wooden frame was successively reinforced with more and more pieces of iron, and in 1825 the complete cast iron plate was introduced by the American piano maker Babcock. The iron plate could withstand the increased string tension, and prevented the instrument from gradually changing shape as the wooden instruments did. Also, it now became possible to keep the tuning stable over longer periods of time.
The hammers of the early pianos were tiny, light pieces made out of leather. However, the introduction of coarser strings at higher tensions demanded larger and heavier hammers. In 1826, felt hammers were tried for the first time by an ingenious piano maker in Paris named Pape. The success was immediate and lasting. An incredible amount of work was devoted to the development and refinement of the actions. A prominent name in this connection is the French piano manufacturer Erard who invented the so-called double repetition action in 1821, which is the type of action still used in the grand piano. The construction was refined by another French manufacturer named Herz around 1840. Smaller improvements were made during the following decades, but since then no essential changes have been made. A simpler type of action, the Viennese action, lived a parallel life before it eventually vanished during the first decades of this century.
The compass of the piano has increased successively during its history. Cristofori's piano had only four octaves. Today a piano with a standard setup of 88 keys will cover more than seven octaves (A0 = 27.5 Hz to C8 = 4186 Hz), no less than the pitch span of the modern symphony orchestra. Furthermore, the acoustic output at fortissimo - small as it might seem (of the order of 0.1 W) - surpasses all other string instruments. This power is enough to fight even the largest ensemble (although brute force not always is the best way of making a solo instrument heard above the orchestra).
The early pianos were of the type we now call a grand piano. During the 19th century the manufacturers discovered a market for smaller and cheaper models, and squares and uprights were constructed, both instruments being economy versions of the "real" piano and filled with compromises. Both the grand and upright pianos as we know them today developed during the 19th century, which saw a wealth of patent applications during its latter half. The period of development declined shortly before the turn of the century, indicating that the construction was perfected, at least for the time being.
Several of the recognized piano makers have had a long tradition including connections with famous composers. Mozart played a Stein piano from Austria, Beeethoven preferred an English Broadwood, and Chopin's piano was made by Pleyel in France - instruments from eminent makers which today, however, are out of business or operating on a very low level. Liszt and Wagner, on the other hand, used grands from Steinway & Sons (New York, Hamburg) which were very close to the instruments we still are used to hearing 100 years later. Other old, recognized piano manufacturers still in operation are Bösendorfer (Vienna), Bechstein (Berlin), Baldwin (USA) and Yamaha (Japan).
The 20th century has been rather quiet as regards the development of the piano, but a dramatically increased production has manifested itself in an undesirable way. The beginnings of a lack of suitable wood and felt for piano purposes can be discerned. This will successively put pressure on the manufactures to search for new materials which can replace the traditional ones. This could, or probably will, demand changes in the design of several major parts in the piano, and the possibility of an active period of development like the one a century ago cannot be ruled out.
Today, the piano is challenged by synthesizers, especially so the economy versions of upright pianos. These pianos do not perform particularly favorably either in price or in tone quality compared to dedicated piano synthesizers ("digital pianos, samplers"). Still, the production of traditional pianos is large, estimated at 900 000 instruments a year worldwide (1988). In particular, the grand piano seems to continue to attract professional keyboard players of all genres, apparently for a number of reasons. Although the quality of the sound probably is the main cause of its fascination, the mechanical response from the instrument via the keys and the vibrating structure also seems to be very important.
In view of the rapid development of new instruments based on digital sound generation, it is tempting to speculate about the future for the piano and the other traditional instruments. It seems reasonable to suppose that the singing voice will be recognized as a musical instrument as long as we use speech in communication. The vowels in speech and singing will familiarize us with harmonic sounds, i. e. sounds which are associated with a distinctive pitch. As long as pitch is used as a mean of communication in music, string and wind instruments will take an exclusive position, because strings and pipes are the only tools available for generating such sounds mechano-acoustically. A piano-like instrument with struck strings could thus be assumed to be a natural member also of a future instrument inventory, should the traditional way of generating sounds survive.
However, it is also possible that in the future most music will be performed on electronic devices. This technique gives a much wider freedom in designing the sounds, including imitation of the traditional instruments. Such imitations could also include extrapolations to new pitches and dynamic levels, not accessible by the original instruments. It is hard to deduce a priori if the piano sounds belong to the group of traditional musical sounds which will survive in the long run, when transferred to a family of new instruments. However, in view of the present popularity of the piano and recognizing the slow change in taste of musical sounds hitherto, it is an advanced guess that pianolike sounds will be used and enjoyed for at least another century.
In this section, a survey of basic piano acoustics is given for those of the readers who want an introduction to the lectures. The fundamental principles which govern the acoustics of the piano are presented in a somewhat simplified form. A detailed and more realistic story of the sound generation in real pianos follows in the lectures.
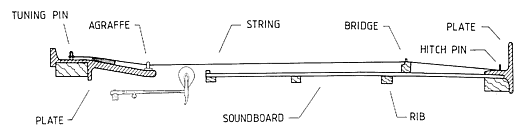
A schematic view of the piano is shown in Fig. 1.
A steel string is suspended under high tension between two supports (the agraffe or capo d'astro bar and the hitch pin) fastened in the metal frame (the plate). Close to the hitch pin end, the string runs across a wooden bar, the bridge, which is glued to a large and thin wooden plate, the soundboard. The level of the bridge is slightly higher than the string terminations, thus causing a downbearing force on the bridge and the soundboard. The soundboard is reinforced by a number of ribs glued to the underside, one reason being to make the soundboard withstand the downbearing force. The string is struck by a felt hammer, which gains its motion from the key via a complicated system of levers, the action.
Fig. 1. Principal sketch of the piano, designating the main components.
Physically, the string motion can be described in the following way. As the hammer strikes the string, the string is deformed at the point of collision (see Fig. 2). The result is two waves on the string, travelling out in both directions from the striking point The wavefronts enclose a pulse, or hump, which gradually gets broader.
Fig. 2. The evolution of the propagating pulse on the string after hammer impact.
However, as the string is struck close to its termination at the agraffe, one of the wavefronts (the one travelling to the left in the figure) soon reaches this end and is reflected. The reflection at a rigid support makes the wave turn upside down. This inverted wave starts out to the right and restores the string displacement to its equilibrium level.
The surprising situation has now developed that the wavefront initially travelling to the left in the figure, has turned into the trailing end of a pulse of fixed width, propagating to the right towards the bridge. At the bridge, the entire pulse is reflected, the effect being that the pulse starts out in the opposite direction upside down. A new reflection at the agraffe turns it right side up again, and soon the pulse has completed one round trip and continues out on the next lap. If the key struck happens to be A4 = 440 Hz ("concert A"), the pulse completes 440 such round trips per second.
The propagation velocity of the pulse on the string is determined by the tension and mass per unit length of the string, a higher velocity the tauter and lighter the string. The number of round trips per second, the fundamental frequency (closely related to the perceived pitch), also depends on the distance to be covered - the longer the string the longer the round trip time (fundamental period), and hence, the lower the pitch. The pitch of a string is thus determined by a combination of its length, tension, and mass per unit length. In particular, string length can be traded off against mass per unit length in order to reduce the size of the instrument. This can be seen in the bass section, where the strings are wrapped with one or two layers of copper in order to make them heavy and thus relatively short. The advantage of a wrapped string over a plain string is that the mass can be increased without reducing the flexibility drastically. A piano string need not be perfectly flexible, but a too stiff a string would have a detrimental influence on the tone quality as will explained below
A piano string, like all other strings, has a set of preferred states of vibration, the resonances, or modes of vibration (see Fig. 3). When a string is vibrating at one of its resonances, a condition which usually only can be reached in the laboratory, the motion of the string is of a type called sinusoidal. The corresponding sound is a musically uninteresting sine wave. In normal use, however, where the string is either struck, plucked or bowed, all resonances are excited, and the result is a set of simultaneously sounding sine waves, partials, forming a complex tone.
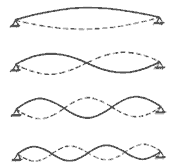Fig 3. The four lowest modes (resonances) of a rigidly supported string. Sometimes these elementary states of vibration are referred to as standing waves, because the amplitude contour does not change with time.
Such a tone is conveniently described by its spectrum, which shows the frequencies and strengths (amplitudes) of the partials (see Fig. 4, bottom). As mentioned, the pitch of the tone is related to the frequency of the lowest member in the spectrum, the fundamental. To be more specific, it is the frequency spacing between the partials - which for a piano tone is closely the same as the fundamental frequency - which is the closest physical correlate to the perceived pitch. The relations between the amplitudes of the partials and their evolution in time contribute to our perception of tone quality.
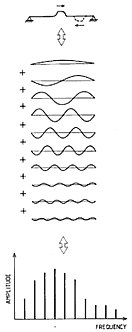Fig. 4. Schematic illustration of the equivalence of the pulse motion on the string (top) and a sum of the string modes (resonances) (middle). The properties of the tone are conveniently summarized by its spectrum (bottom), showing the frequencies and amplitudes of the components (partials).
The pulse running back and forth on the piano string has a most surprising connection to the string modes (resonances). It can be shown mathematically that the travelling pulse is made up of a sum of all the string modes! The shuttling pulse and an (infinite) sum of string modes of appropriate amplitudes are equivalent; they are just two ways of representing the same phenomenon (cf. Fig. 4). So while our eyes will detect the pulse motion (if slowed down enough by the use of a stroboscope) our ears prefer to analyse the string motion in terms of its partials or Fourier components, so named after the French mathematician who first described this equivalence.
Fourier also stated that if the motion is periodic, that is, the same events will repeat indefinitely with regular intervals, the frequencies of the corresponding partials will be harmonic. This means that the frequency ratios between the partials will be exactly 1 : 2 : 3 : 4 . . . , which will be perceived as a sound with a clearly defined pitch and steady tone quality. The statement can also be turned the other way around; if the resonance frequencies of a string are strictly harmonic, the resulting motion of the string will always be periodic.
In real pianos, the resonance frequencies of the strings are not exactly harmonic. The frequency ratios are slightly larger than 1 : 2 : 3 : 4 . . . , more like 1 : 2.001 : 3.005 : 4.012 . . . , which is referred to as inharmonicity. The inharmonicity in piano strings, which is caused by the bending stiffness of the steel wire, is a desirable property as long as it is kept within limits. According to Fourier, the string motion will now not repeat exactly periodically as the note decays, but change slowly which gives a "live" quality to the note.
Returning to the excitation of the string by the hammer impact, not only the amplitude of the initial pulse on the string changes with the strength of the blow, but also its shape. This is due to a remarkable property of the felt hammer, more specifically the characteristics of its stiffness. The stiffness increases (the hammer becomes progressively harder to compress) the more the hammer already has been compressed, a phenomenon referred to as nonlinear stiffness. This means that a harder blow not only will give a larger amplitude but also sharper corners of the pulse on the string. Again, according to Fourier, sharper wiggles in the waveform correspond to more prominent high frequency partials in the spectrum. Consequently, the piano tone will attain a different ("more brilliant") tone quality at forte (loud) compared to piano (soft).
The vibrating string contains all the partials we would like to hear, but unfortunately the string is in effect unable to radiate sound. The difficulty is well described by the English saying: "You can't fan a fire with a knitting needle!" The reader may easily verify this statement by making the experiment, but can also notice that by means of a large object like a tray instead of the needle, it is quite possible to fan a fire even from a distance. The point is that a certain flow of air must be pumped back and forth per second in order to radiate a "fan wave."
This can be achieved with a limited motion of the tray having a large cross section, while the needle would have to make unreasonably large movements to reach the same effect. The acoustic engineer would "explain" the situation by saying that the radiation resistance of the tray is much higher than that of the needle. In other words, because of its larger area, the tray is much better than the needle as a transmission link between the motion of the arms and the motion of the air.
Returning to the piano, we now realize that as the thin string cannot radiate a sound wave itself, its motion has to be transferred to a much larger object which can serve as a more efficient radiator of sound. This is readily done by incorporating a soundboard in the design, including a bridge as a connecting element to the string(s). But now the piano designer meets with a new difficulty. The soundboard is much heavier than the string, which means that the string will not be able to vibrate the soundboard efficiently and the vibrational energy will still be trapped in the string. Only slowly the energy will leak into the soundboard during repeated reflections of the string pulse at the bridge.
In engineering terms, there is a mismatch between the mechanical impedance of the string and that of the soundboard. The mechanical impedance is a property that tells us to what degree an object resists (impedes) motion. From the point of view of the string, the soundboard has a very high (input) impedance; it can be thought of as a very heavy stone, or a very stiff spring, which must be vibrated vigorously. The experienced reader will certainly agree that this is a most uncomfortable task with little chance of success.
However, conditions can be improved, or in other words, the impedance mismatch can be diminished, by increasing the (characteristic) impedance of the string. This is easily done by making it heavier and by increasing its tension. But a heavier string usually means a thicker string, which automatically gives a higher stiffness and hence more inharmonicity, which soon spoils the desired piano timbre. Piano designers circumvent this problem in two ways, either by wrapping a rather thin steel core with copper (which also influences the pitch as mentioned), or by "splitting" a thick plain string into two or three strings, tuned to (almost) the same frequency, a technique called multiple stringing. Now the vibration energy is transmitted more efficiently from the string(s) into the soundboard and the note sounds louder, perhaps "too" loud. Because here the next difficulty appears; the gain in loudness does not come for free.
It stands to reason that the pianist cannot feed energy continuously to the string like the violinist via the bow. Consequently the piano tone is condemned to decay and die. The question is then how to spend the energy quantum delivered at the key stroke in the best way. If a loud and thus necessarily shorter note is desired, the impedance mismatch between string and soundboard should be decreased by making the strings heavier and tightening them even harder.
On the other hand, the note can be made longer by using lighter and less tense strings, but at the expense of loudness. The trade-off between loudness and duration, or "sustain," of the tone is a difficult problem in piano design, especially as the impedance of the soundboard can vary wildly from note to note, due to its inherent resonances. It is easy to get a piano in which some notes are loud and short while adjacent notes are much softer and longer, a musically most unsatisfying situation. Fortunately, such fluctuations between notes as well as the basic conflict between loudness and sustain can be alleviated in an almost miraculous way by multiple stringing, a phenomenon which is covered in detail in one of the lectures.
The soundboard radiates sound much better than the strings do, as mentioned, but nevertheless it has several severe shortcomings. One occurs at very low frequencies and is due to the fact that both sides of the soundboard are directly exposed to the surrounding air.
The reason is the following.
Let the soundboard be moving upwards, pushing the air above its upper surface together. This causes a temporary excess of air molecules in a region above the soundboard, a compression, corresponding to an increased pressure. The underside of the soundboard is also moving upwards, so there is at the same moment a temporary loss of air molecules beneath the soundboard, a rarefaction, corresponding to a reduced pressure. As nothing prevents the compressed air on the upper side from flowing into the lower region, this pressure difference will soon be neutralized. Half a period later, when the soundboard is moving downwards, the process repeats but now the air flows from the lower to the upper side. So, at low enough frequencies - as long as the motion of the soundboard is slow enough to allow the exchange of air to take place before the direction of its motion has reversed -the soundboard will uselessly pump air from its upper side to its lower side and back again instead of radiating sound. The phenomenon is called acoustic short-circuiting, and can be avoided by separating the two radiating sides of the soundboard by an (almost) closed sound box, as in the guitar or in most harpsichords.
A similar phenomenon can be observed also at higher frequencies. Now the soundboard no longer vibrates as a unit but spontaneously divides into smaller vibrating areas separated by thin regions of no motion (nodal lines). Depending on frequency, the vibrating areas form different patterns; the higher the frequency, the smaller and so the more numerous are the areas. These preferred states of vibration are called the eigenmodes (modes), or often, the resonances, of the soundboard. Adjacent vibrating areas vibrate in what is called opposite phase, which means that while one area is moving upwards its neighbour is moving downwards and vice versa. Also in this case, it is easy to imagine that a useless exchange of air between adjacent areas can occur instead of the desired sound radiation.
This closes the short survey of basic piano acoustics. Once again, it is to be understood that the explanations are simplified, dealing only with the basic aspects of the phenomena. Against this background, the lectures that follow will illustrate the wealth of complications which arise in real instruments.
In this volume, the use of metric (SI) units is encouraged. While the use of meters and kilograms probably will cause English and American readers only minor problems, the force unit Newton (N) might be less familiar. As a rule of thumb, 1 N corresponds to the weight of an apple (mass 100 g)!(***) Likewise, 10 N corresponds approximately to the weight of a mass of 1 kg, for example 1 litre (1 US quart) of milk.
The naming of octaves and pitches follows the straightforward nomenclature given by American standards. In this notation the "middle octave" is indicated by number four (middle C = C4). The lowest note on full size piano is A0 and the highest C8.
After these introductory passages, it is time for a detailed voyage into the world of the acoustics of the piano, guided by experts in the different areas. The lectures follow in the same (logical) order as they were given on the seminar day, but as the contributions are essentially independent the readers may feel free to follow their own paths.
In the first lecture, Harold Conklin, an experienced piano design engineer, outlines the design principles of the parts of the piano, and makes comparisons between the early and the modern instruments.
Secondly, Anders Askenfelt and Erik Jansson, researchers in music acoustics with a focus on string instruments, present measurements from the initial steps in the tone production, from the moment when the pianist touches the key up to and including the string vibrations.
Then follows a theoretical study by Donald Hall, a physics professor with a strong personal interest in keyboard instruments, who describes a computer model of what actually happens during the collision between the hammer and the string, and the implications for the string vibrations.
The decay of the piano tone, and in particular the influence of multiple stringing is covered next by Gabriel Weinreich, also a physics professor with a strong interest in music acoustics.
Finally, the sound radiation and its connection to the properties of the soundboard are described by Klaus Wogram, a researcher with many years of experience in investigating musical instruments, in particular brass instruments and the piano
Notes
(*) Hermann von Helmholtz: Die Lehre von Tonempfindungen als physiologische Grundlage für die Theorie der Musik, first edition 1862, English translation of the fourth edition in 1885 by A. J. Ellis: On the Sensations of Tone as a Physiological Basis for the Theory of Music, reprinted (paperback) by Dover Publications Inc., New York 1954.
(**) It is true that also the harpsichord can be played at somewhat different dynamics depending on how the key is depressed. Compared to the piano, however, the dynamic range is narrow, and dynamics are usually not prescribed in harpsichord music.
(***) This useful remark was given by one of the lecturers (G. Weinreich) on an earlier occasion.
This introduction is a part of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music