[< Previous] [Contents of this lecture] [Next >]
We can now proceed and compare the string motion and corresponding spectra in the bass, mid and treble sections, respectively (see Fig. 16).
The pulse pattern on the string, described above for a midrange note (Fig. 15), is in fact even more pronounced for the bass notes. Due to the relatively short excitation pulse in comparison to the fundamental period (cf. Fig. 8), a bass string remains at rest for a long period of time before the first reflected pulse returns. Surprisingly, the returning pulse is foreboded by a ripple-like motion with growing amplitude. This behavior is caused by a strange phenomenon called dispersion, which is a manifestation of the stiffness of the string. As discussed in the Introduction to this book, the propagating pulse is made up of many Fourier components (partials), each with its own frequency. Due to the stiffness, those Fourier components with high frequencies propagate with slightly higher velocity and thus returns a little earlier, which causes the spread of the pulse.
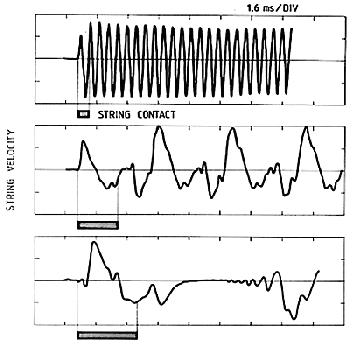Fig. 16. Comparison of the string waveforms (velocities) for treble (C7, top), mid (C4, middle) and bass notes (C2, bottom) played mezzo forte. The pulse character of the string motion is clearly seen for the bass note, while completely obscured in the treble.
The string motion in the treble is very different from the pulses observed in the mid and bass sections. This is due to the width of the initial pulse, which is so long in relation to the round trip time on the string, that it is no longer possible to observe individual pulses. The outgoing and reflected pulses get mixed up and form a pattern resembling a standing wave.
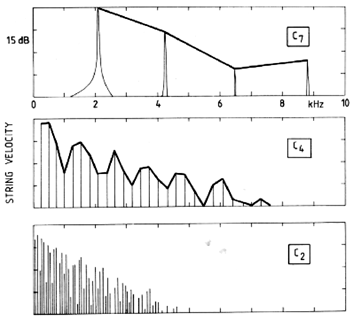Fig. 17. The corresponding spectra for the notes in Fig. 16. The treble note (top) shows only a few partials but these reach high frequencies. The bass note on the other hand (bottom), is rich in partials, but they do not extend very high in frequency.
The corresponding spectra for the bass, mid and treble notes also show interesting differences (see Fig. 17). As predicted in the discussion of the hammer-string contact durations, the treble contains only few partials, but these reach high frequencies (about 10 kHz for the treble note in Fig. 17). The middle register note contains more partials, up to approximately 7 kHz. The bass is very rich in partials, but on the other hand they do not extend beyond 4 kHz. These dramatic spectral differences reflect the present preferences of the piano designer.
By changing the hammer properties, remarkable differences in spectra can be obtained (see Fig. 18). The three spectra in this figure all refer to middle C (C4), struck with different hammers. By means of a treble hammer (C7) the spectrum can be extended beyond 10 kHz, compared to the normal 7 kHz. With a bass hammer (C2) on the other hand, the spectrum is cut off at approximately 4 kHz. Apparently none of these extremes are appreciated by the manufacturers of today (or the customers).
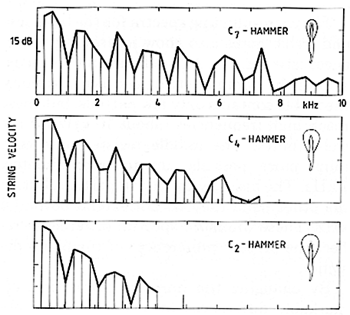Fig. 18. Spectrum of the note C4 (mf), illustrating the influence of hammer properties. The original hammer (middle) is replaced by a treble hammer (C7, top) and a bass hammer (C2, bottom). Note that the spectral changes are substantial, resembling the spectral differences between bass - mid - treble in Fig. 17.
[< Previous] [Top] [Contents of this lecture] [Next >]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music