
String contact duration and dynamic level
[<- Previous]
[Contents of this lecture]
[Next ->]
A second interesting observation that can made from Fig. 4 is that the duration of the hammer-string contact decreases as the dynamic level is raised. This is due to a peculiar property of the piano hammer, called nonlinear stiffness. In effect, this nonlinearity makes the hammer harder, the higher the impact velocity. The details of this effect which is of extreme importance for a proper tone generation, is explained in the lecture by Donald Hall.
At the moment it may suffice to know that the duration of the hammer-string contact time is one of the major parameters in determining the spectral content. It can be shown that a shorter contact duration increases the amount of high frequency partials in the spectrum. The graph in Fig. 6 illustrates how the contact duration decreases with rising level for a note in the midrange, indicating a boost of the high-frequency partials when the dynamic level grows from piano to forte. The variation in contact duration within a comfortably accessible dynamic range (p - ff) is about +/- 20 % compared to mezzo forte. Later in this presentation we will return to measurements of the spectral changes which follow from changes in dynamic level.
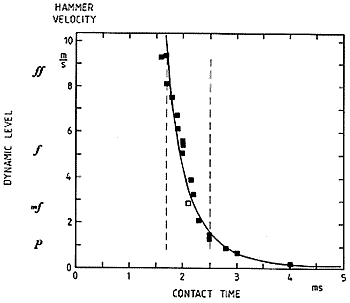 Fig. 6. Illustration of the how string contact duration decreases with rising dynamic level (C4). A touch by a pendulum (mf) is represented by an unfilled square. The dashed lines represent the range in contact duration covered in a comfortably accessible dynamic span from p to ff.
Fig. 6. Illustration of the how string contact duration decreases with rising dynamic level (C4). A touch by a pendulum (mf) is represented by an unfilled square. The dashed lines represent the range in contact duration covered in a comfortably accessible dynamic span from p to ff.
Given a fixed dynamic level, the contact duration is determined by such design factors as the ratio between the mass of the hammer and the string(s) and the striking point along the string. As these parameters vary over the compass of the piano, the contact durations will change slowly from bass to treble. In Fig. 7, the contact durations are sampled by one note per octave, and as we can see the contact durations decrease from about 4 ms in the bass to less than 1 ms in the highest treble. Not surprisingly, the treble could thus be assumed to contain spectral components with higher frequencies than the bass.
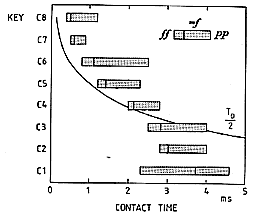 Fig. 7. Hammer-string contact durations expressed in milliseconds, illustrating how the contact durations decrease from bass to treble. The bars indicate the range in contact duration between a blow in ff (left end) and pp (right end). The vertical line in each bar represents a blow by a pendulum at mezzo forte. The solid curve marked To/2 represents half a period of the fundamental.
Fig. 7. Hammer-string contact durations expressed in milliseconds, illustrating how the contact durations decrease from bass to treble. The bars indicate the range in contact duration between a blow in ff (left end) and pp (right end). The vertical line in each bar represents a blow by a pendulum at mezzo forte. The solid curve marked To/2 represents half a period of the fundamental.
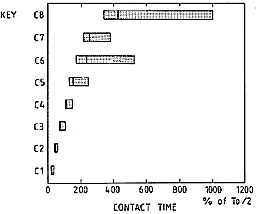 Fig. 8. The same hammer-string contact durations as in Fig. 7, but now expressed in percent of half a period of the fundamental (To/2). Note that in this relative measure, the durations are short in the bass and long in the treble.
Fig. 8. The same hammer-string contact durations as in Fig. 7, but now expressed in percent of half a period of the fundamental (To/2). Note that in this relative measure, the durations are short in the bass and long in the treble.
An entirely different picture develops if the contact durations are related to the period time of the fundamental (the inverse of the fundamental frequency) of the corresponding note (see Fig. 8). Now it can be seen that the contact durations are short in the bass in comparison with the fundamental period, while the opposite situation prevails in the treble.
A general theorem in string physics helps us to interpret these differences. The theorem tells us that string resonances with period times essentially shorter than the contact duration will be only weakly excited by the blow. The implication of this theorem for the sound quality of the piano is that the bass notes will be rich in partials compared to the treble notes. This is so, because in the bass the contact duration is only about 10 % of the fundamental period; it is not until the 10th partial that we reach a period time that is short in comparison with the contact duration. In the treble on the other hand, even the fundamental period is much too short to be optimally excited, and the situation for the higher partials becomes successively worse.
An alternative design of the piano could be imagined, such that the string contact durations were a constant fraction of the fundamental period over the entire compass. This would demand a rescaling of the striking points, much heavier bass hammers than "normal," and also lighter treble hammers. However, the sound would probably be rated as second to the present design, being too muddy in the bass and too brilliant in the treble.
In this case the customers are likely to have good acoustical reasons to reject the new design. But even in the case of smaller changes which would be welcomed by the manufacturer, the customers are notoriously hard to convince about the benefit of news. Tradition bears a strong power on music and musical instruments. Imagine a traditional piano concerto being played on anything but a black grand piano!
[<- Previous]
[Top]
[Contents of this lecture]
[Next ->]
This lecture is one of Five lectures on the
Acoustics of the piano
© 1990 Royal Swedish Academy of Music
 Fig. 6. Illustration of the how string contact duration decreases with rising dynamic level (C4). A touch by a pendulum (mf) is represented by an unfilled square. The dashed lines represent the range in contact duration covered in a comfortably accessible dynamic span from p to ff.
Fig. 6. Illustration of the how string contact duration decreases with rising dynamic level (C4). A touch by a pendulum (mf) is represented by an unfilled square. The dashed lines represent the range in contact duration covered in a comfortably accessible dynamic span from p to ff.

 Fig. 7. Hammer-string contact durations expressed in milliseconds, illustrating how the contact durations decrease from bass to treble. The bars indicate the range in contact duration between a blow in ff (left end) and pp (right end). The vertical line in each bar represents a blow by a pendulum at mezzo forte. The solid curve marked To/2 represents half a period of the fundamental.
Fig. 7. Hammer-string contact durations expressed in milliseconds, illustrating how the contact durations decrease from bass to treble. The bars indicate the range in contact duration between a blow in ff (left end) and pp (right end). The vertical line in each bar represents a blow by a pendulum at mezzo forte. The solid curve marked To/2 represents half a period of the fundamental.
 Fig. 8. The same hammer-string contact durations as in Fig. 7, but now expressed in percent of half a period of the fundamental (To/2). Note that in this relative measure, the durations are short in the bass and long in the treble.
Fig. 8. The same hammer-string contact durations as in Fig. 7, but now expressed in percent of half a period of the fundamental (To/2). Note that in this relative measure, the durations are short in the bass and long in the treble.