[<- Previous] [Contents of this lecture] [Next ->]
The typical decay of a piano tone is shown in Fig. 1, which displays the sound pressure level as a function of time. We see that the string is struck by the hammer at about t = 2 seconds, and the damper is released, stopping the vibration, at about t = 17 seconds. The vertical scale is in decibels, so that the ordinate of the graph is proportional to the logarithm of the pressure amplitude. In such a plot, the drop in level would appear as a straight line if the decay of the sound were of a type called exponential, which is what a physicist would expect from a linear system such as the string and the soundboard. Instead, it is clear that the curve breaks into two portions of quite different decay rates. The initial portion, called "prompt sound," drops (in this case) at a rate of about 8 dB/sec; the final one, called "aftersound," at less than one-quarter that rate. As we shall see, the prompt sound is simply related to the theoretical decay rate determined by the string's coupling to the soundboard; whereas the aftersound, which gives the piano its perceived sustaining power, represents the "miracle."
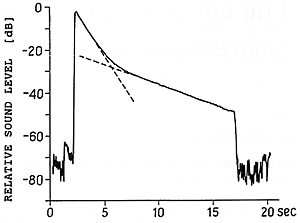Fig 1. Typical decay of a piano tone as illustrated by the sound pressure level versus time (Eb3 = 311 Hz). The decay process is divided into two parts; an initial attack part with a fast decay ("prompt sound") followed by a sustained part with slow decay ("aftersound").
The most interesting factor contributing to the existence of aftersound is the presence of more than one string for each piano note, and the consequent dynamical coupling that occurs among the strings struck by the same hammer. In the case of Fig. 1, however, we are dealing with a simpler phenomenon, since in this particular experiment only one of the three strings belonging to this note (Eb4) was allowed to sound. It should also be added that the curve in Fig. 1 was obtained by taking the signal produced by a microphone and filtering out all but the fundamental frequency; the complex decay pattern can not, in other words, be attributed to variously decaying partials (although such a factor may contribute to the way the overall note is perceived). Rather, the behavior of the decaying curve in Fig. 1 is explained by noting that even a single string vibrating at its fundamental frequency has two distinct modes of vibration corresponding to two possible directions of vibration (polarization); "vertical" and "horizontal." Here, we use the adjectives appropriate for a grand piano although the same phenomenon of course takes place also in the upright piano.
What is happening here is that the vertical polarization is the primary one excited by the hammer, and so begins its life at a much higher amplitude than the horizontal one. However, since the bridge, which is attached to the soundboard, "gives" much more easily in the vertical than in the horizontal direction, the decay of the vertical mode is also much more rapid. As a result, the relatively slight amount of horizontal vibration becomes, after a while, dominant.
Although this hypothesis can be verified by direct observation of the string vibration, it is interesting to approach it in a somewhat different way. In Fig. 2, we show another graph of sound level versus time (again at the fundamental frequency) which was obtained by the same procedure as Fig. 1 except that the location of the microphone is different. The data indicate clearly that we are dealing with two independent modes of vibration, which are producing sound waves through two separate radiating "antenna patterns." When one or the other mode dominates - that is, either near the beginning or near the end of the note - the two graphs show identical behavior; but when the modes radiate with approximately equal amplitude, they can add either "constructively" or "destructively," depending on microphone placement.
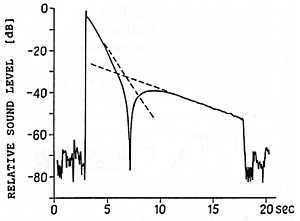Fig. 2 The decay of the same note as in Fig. 1 but recorded at a different microphone position. A comparison with Fig. 1 reveals the existence of two components in the sound field, radiated by the vertical and horizontal soundboard motions respectively. The two components are of equal strength during an interval around the intersection of the sloping lines. In this region the resulting sound level varies strongly with microphone position.
In fact, it is quite reasonable to suppose that the vibration pattern of the soundboard in response to a vertical force at the bridge is quite different from what it is for a horizontal force; and since at this frequency at about 311 Hz the wavelength of the sound is of the order of 1 meter, comparable to the size of the piano, the directional radiation pattern for the two can easily be quite different.
[<- Previous] [Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music