
av
Anders Friberg
Akademisk avhandling som med tillstånd av Kungliga Tekniska Högskolan
i Stockholm framlägges till offentlig granskning för avläggande
av teknologie doktorsexamen fredagen den 26 maj kl 14.00 i kollegiesalen,
Valhallavägen 79, KTH, Stockholm. Avhandlingen försvaras på
engelska.
This is the summary part of my thesis. The other parts that are included in the printed version are listed in the section Included Parts below. The music examples on the CD-ROM, referred to in the summary, are the same as the examples found on the Music Performance web page. The errata of the original edition and a few other minor misprints are included in this text. No other changes has been done.
Anders Friberg, Stockholm 1997
Contents
The dissertation consists of a summary and the following parts.
| Paper I. | Friberg, A. (1991). Generative Rules for Music Performance: A Formal Description of a Rule System. Computer Music Journal, 15 (2), 56-71. |
| Paper II. | Friberg, A., Frydén, L., Bodin, L.-G., and Sundberg, J. (1991). Performance Rules for Computer-Controlled Contemporary Keyboard Music. Computer Music Journal, 15 (2), 49-55. |
| Paper III. | Friberg, A., Sundberg, J. & Frydén, L. (1994). Recent musical performance research at KTH. in J. Sundberg (ed.), Proceedings of the Aarhus symposium on Generative grammars for music performance1994, 7-12. |
| Paper IV. | Friberg, A., & Sundberg, J. (1995). Time discrimination in a monotonic, isochronous sequence. J. Acoust. Soc. Am., 98(5), pp. 2524-2531. |
| Paper V. | Sundberg, J., Friberg, A. & Frydén, L. (1991). Threshold and preference Quantities of Rules for Music Performance. Music Perception 9 (1), 71-92. |
| Paper VI. | Friberg, A., & Sundberg, J. (1994). Just Noticeable Difference in duration, pitch and sound level in a musical context. in I. Deliège (ed.), Proceedings of 3rd International Conference for Music Perception and Cognition, Liège 1994, 339-340. |
| Paper VII. | Sundberg, J., Friberg, A. & Frydén, L. (1992). Music and locomotion. A study of the perception of tones with level envelopes replicating force patterns of walking. Speech Transmission Laboratory Quarterly Progress and Status Report, 4/1992, 109-122. |
| CD-ROM | Friberg, A., Sundberg, J. & Frydén, L. (1994). "Director Musices Demo 1.2" and "Music Examples", in Section The Art of Playing, in Information Technology and Music, CD-ROM, produced by the Royal Swedish Academy of Engineering Science. |
The papers will be referred to by their Roman numerals. Figures and
tables will be referred to by the Roman numeral and the number in the paper.
A rule system is described that translates an input score file to a musical performance. The rules model different principles of interpretation used by real musicians, such as phrasing, punctuation, harmonic and melodic structure, micro timing, accents, intonation, and final ritard. These rules have been applied primarily to Western classical music but also to contemporary music, folk music and jazz. The rules consider mainly melodic aspects, i. e., they look primarily at pitch and duration relations, disregarding repetitive rhythmic patterns. A complete description and discussion of each rule is presented. The effect of each rule applied to a music example is demonstrated on the CD-ROM. A complete implementation is found in the program Director Musices, also included on the CD-ROM.
The smallest deviations that can be perceived in a musical performance, i. e., the JND, was measured in three experiments. In one experiment the JND for displacement of a single tone in an isochronous sequence was found to be 6 ms for short tones and 2.5% for tones longer than 250 ms. In two other experiments the JND for rule-generated deviations was measured. Rather similar values were found despite different musical situations, provided that the deviations were expressed in terms of the maximum span, MS. This is a measure of a parameter's maximum deviation from a deadpan performance in a specific music excerpt. The JND values obtained were typically 3-4 times higher than the corresponding JNDs previously observed in psychophysical experiments.
Evaluation, i. e. the testing of the generality of the rules and the principles they reflect, has been carried out using four different methods: (1) listening tests with fixed quantities, (2) preference tests where each subject adjusted the rule quantity, (3) tracing of the rules in measured performances, and (4) matching of rule quantities to measured performances. The results confirmed the validity of many rules and suggested later realized modifications of others.
Music is often described by means of motion words. The origin of such
analogies was pursued in three experiments. The force envelope of the foot
while walking or dancing was transferred to sound level envelopes of tones.
Sequences of such tones, repeated at different tempi were perceived by
expert listeners as possessing motion character, particularly when presented
at the original walking tempo. Also, some of the character of the original
walking or dancing could be mediated to the listeners by means of these
tone sequences. These results suggest that the musical expressivity might
be increased in rule-generated performances if rules are implemented which
reflect locomotion patterns.
Keywords: music, performance, expression, interpretation, rules, computer
music, midi, jnd, time discrimination, locomotion, motion, listening test
| deadpan performance | performance in which all parameters are set at their nominal values |
| nominal time or nominal duration | the duration given from the score in the given tempo, assuming simple integer relations for the different note values. |
| ET | Equal Temperament |
| JND | Just Noticeable Difference |
| MS | Maximum span in a music excerpt of a given physical parameter. |
| K, k, Q | the general quantity parameter available for each rule. |
| duration | duration from the onset to next onset, see also DR, Fig I.1 |
| offset to onset duration | micro pause duration between two consecutive notes, see also DRO, Fig. I.1 |
Interpretation is one of the most important aspects of music performance. It can be described in terms of deviations from the notated score. Such expressive deviations have been frequently studied almost as long as tools have been available to measure them (see Gabrielsson, forthcoming). From such measurements it would be possible to deduce general performance features and principles, if such existed. There are in fact good reasons to assume that such principles do exist (Palmer, 1989; Clarke, 1988; and cf. Sloboda 1985). However, rather few general principles have been revealed during the past. A major problem is that a specific deviation on one note could originate from several different principles, so the "true" origin may be impossible to trace. It is difficult to identify a multidimensional structure underlying a surface level, merely by analyzing this surface level.
An alternative strategy has been applied here, namely analysis-by-synthesis. This means that we start with a hypothesized principle, realize it in terms of a synthetic performance, and evaluate it by listening. If needed, the hypothesized principle is further modified and the process repeated. Eventually, a new rule has been formulated. In other words, the method is to teach the computer how to play more musically. The success of this method is entirely dependent on the formulation of hypotheses and on competent listeners. An important condition for the success of our project has been our longtime co-operation with the expert musician and educator Lars Frydén. Essential factors have been his ability to formulate hypotheses and to break down the task into its components, and his expertise in listening evaluations. The result is the rule system for musical performance that is presented here. The rules cover many different aspects such as phrasing, punctuation, harmonic and melodic structure, micro timing, accents, intonation, and final ritard. The definitions of the rules can be found in Papers I-III.
The use of direct synthesis requires a flexible computer environment. Originally, a modified version of a text-to-speech system was used (Carlson & Granström, 1975). Later it became necessary to develop a new program specifically designed for experimenting with rules for musical expression. This program, Director Musices, was written by the author and is supplied on the CD-ROM together with its documentation. Music examples demonstrating the effects of all major rules are also included in the CD-ROM, whereby different rule quantities can be selected. Graphs showing the resulting parameter changes accompany the examples. Parts of the rule system have been implemented in other programs (Bresin, 1993; Hansson, 1994; van Oosten, 1993)
When the analysis-by-synthesis method is used, evaluation, in particular the testing of the generality of rules and principles, becomes important. The following methods have been used for the evaluation: (1) listening tests with fixed rule quantities (Paper II; Friberg et al., 1987; Frydén et al., 1988; Thompson et al. 1989); (2) rule quantity preference tests where each subject adjusted the amount of the effect to his/her preferred value (Paper V and III), (3) tracing the rules in measured performances, and finally (4) matching the rule parameters to measured performances (Paper III).
Just noticeable differences (JNDs) for different performance parameters in different musical contexts have been investigated in Papers IV, V and VI, i. e., whether the expressive deviations found in performances are perceptible or not, and by whom.
The rules appear to convey information which helps the listener to process the musical signal flow. An interesting aspect then is the choice of acoustic codes, or to be more specific, what factors determine the shape of the deviations. One hypothesis regarding the origin of the musical code was investigated in Paper VII; the envelope of the vertical force component of the foot during walking was transferred to sound level envelopes, and a set of listening experiments was carried out to see if some of the original motion features survived this drastic transfer.
The rules have concurrently been used for the synthesis of singing at our department (Berndtsson 1995). Recently, other researchers have also started to take an interest in the rules. A group around Giovanni De Poli in Padova, Italy, has investigated various means for modeling interaction effects. As we simply add deviations originating from all rules, a given rule has no "knowledge" about the other rules. As a result, unwanted effects occasionally occur. Bresin & Vecchio (1994; also Bresin, 1994) combined the parameters used by the rules with a neural network and made it learn from performances. Another alternative involved using fuzzy algorithms (Bresin et al. forthcoming). Piano-specific extensions of the rule system were found by Battel & Bresin (1994) in studying Brahms' Paganini variations. The combination of our rules and neural networks was also investigated by Schultz (1994). Shelly Katz, Surrey, U. K., has started a research project about "expressivity in computer generated classical music" using Director Musices and the rules as a base.
Several other systems have also recently been built to study music performance. An interesting approach was taken by Widmer (1994) and Katayose & Inokuchi (1993) who let an AI system infer performance rules from measured performances. Other systems for performance research include the RUBATO workstation (Mazzola & Zahorka, 1994) and POCO (Honing, 1990).
For an exhaustive, comprehensive overview of previous performance research
the reader is referred to Gabrielsson (in press) containing about 400 references.
A bibliography of our own papers about the rules is given in Paper III.
References presenting independent evidence, for example in terms of performance
measurements, are given in the discussion of the individual rules.
The entire project started in 1977 when the analog singing machine MUSSE, previously constructed at the department, could be controlled from a mini computer. While MUSSE's ability to replicate sung wowels was excellent, computer produced MUSSE performances revealed that an entire dimension of great musical significance was missing. It should be noted that in the seventies computer generated music performances were rare. The co-operation between Johan Sundberg and Lars Frydén began in 1978. They started to implement rules in a modified version of the text-to-speech system RULSYS (Carlson & Granström, 1975). Later, Anders Askenfelt assisted in the programming. Early versions of many of the current rules were elaborated on that system (Sundberg et al., 1983a, 1983b). When I started to work at the department in 1984 my main task was to organize the existing rule system and to develop a new program Rulle, later Director Musices. The major advantages of the new program were its polyphonic capability, the use of the MIDI format, and the fact that the program could be tailored for instrumental performance.
The work has since then mainly been carried out jointly by Johan Sundberg, Lars Frydén and myself. It has resulted in the ensemble rules and in the more recent additions for punctuation and phrasing. Also, some existing rules were modified and the general rule quantity parameter K (earlier Q) was introduced.
The communication of a composer's mental representation of a piece of
music to a listener can be assumed to contain three major transformations,
as illustrated in Fig. 1: (1) from composer to score (TCS),
(2) from score to performance (TSP), and (3) from performance
to listener (TPL). The music appears in four different representations
in the figure. In addition, the performer has also a mental representation.
Of these, only two are easily accessible to a scientific analysis: the
score and the performance. The performance is assumed to be the sound signal,
i. e. a recording that can be analyzed in terms of physical parameters.
The transformation TSP is done by the performer and is the main
focus of this study.

Fig. 1. From the composer to the listener: the four different music representations and the three corresponding transformations.
It is advantageous to compare a performance to a nominal performance in which the score is simply translated to nominal values of performance parameters; in such a translation simple integer ratios, for instance, are used for converting note values to tone durations. The difference between the actual and the nominal performances constitutes the expressive deviations.
Why do these deviations from the score exist? There are many possible
reasons. First, the score serves primary as an aid for the memorization
and conservation, as well as for the communication from the composer to
the performer. Scores were never intended as exact descriptions of sounding
music. Second, as the composer and the performer are unaware of the measured
physical quantities, the score may serve as a representation of the cognitive
parameters rather than the physical parameters. There is no need to notate
cognitive representations that both the composer and the performer agree
upon. In this sense the score may be more accurate with respect to cognitive
than to physical parameters (Gabrielsson, 1985). Third, over the centuries
the liberty of the musicians to exhibit their own, personal interpretation
of the composer's piece of art has varied, but has rarely been completely
denied by composers. In cases where this liberty was ample, great deviations
from a nominal performance can be expected.
As mentioned above, the main method used for developing the rules was analysis-by-synthesis. It was adapted from speech synthesis research where it is considered as a standard method. It was a natural choice since the system developed for text-to-speech translation could be adapted to a score-to-musical-expression system. Here some aspects of this method will be discussed.
The typical start is an idea which is formulated as a tentative rule in the computer. Then this rule is applied to a music example so that the result can be evaluated by listening. This offers an immediate feedback, often suggesting further modifications. The process is then repeated until a satisfactory performance is obtained. Thus in a sense the system acts as a student acquiring some basic knowledge of music interpretation from an expert teacher.
One requirement of this method is that everything must be quantified. A typical observation has been that the exact quantity of each parameter is crucial for a good performance. In determining the dependence of a rule on a certain parameter, such as note duration, it is generally helpful to find two extremes and then to interpolate linearly between them. If this does not yield an appropriate result a different function, e. g., a power function can be tried. In this way we can successively improve the rule step by step.
Let us consider an exclusive use of the analysis-by-synthesis method to detect its advantages and disadvantages as compared to a strict analysis-by-measurement method.
One advantage is that the perception of the music is directly used in
the development of the rules, similar to how a musician also act as listener
while playing, and use this information as a feedback, see Fig. 2. In analysis-by-measurement,
the listener's viewpoint, or rather the perception of the music, is not
incorporated in the same direct sense.
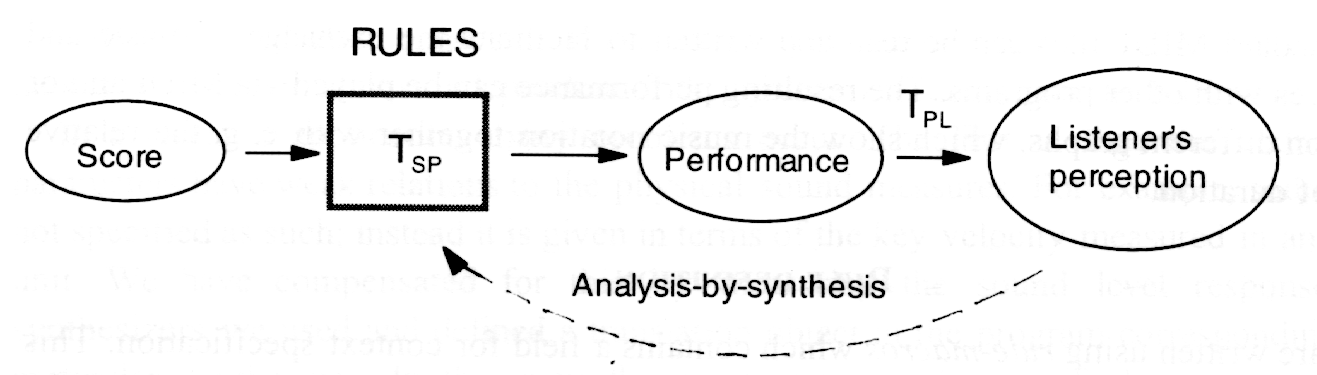
Fig. 2. From score to listener: the rule transformation and the analysis-by-synthesis
loop.
Another advantage is that the general validity of the hypotheses can directly be tested by applying it to other music examples and that the feedback loop is very short between stating the hypothesis and evaluating the results.
A disadvantage is that conclusions are based on the expertise of just a few people. It raises very high demands on the experts that they are competent, consistent, able to focus on a certain aspect of the performance and that they are sensitive also to small deviations. Another disadvantage is that the parameters in the rules can in some cases be chosen rather arbitrarily.
For these reasons the current system was not based solely on the analysis-by-synthesis
method but also on analysis-by-measurement. This is probably quite essential
in performance research. Conversely, as pointed out by Gabrielsson (1985)
it is quite important to complement the analysis-by-measurement method
by listening tests where the deduced principles are applied to synthetic
performances.
The complete current implementation of the rules is included in the Director Musices program. It is a stand-alone program written in Macintosh Common Lisp. The Director Musices Demo 1.2 can be found on the CD-ROM.
The score is coded in a local format specified in the file "MusicFormat" in the Director Musices program directory on the CD-ROM. A short example:
v1
(bar 1 meter (4 4) n (() . 2) rest t q ("E" "G#" "B") modus "min" key "A" mm 112)
(n (() . 4) rest t)
(n ("E4" . 4))
(bar 2 n ("F4" . 8))
(n ("E4" . 8))
(n ("F5" . 4) dot 1)
(n ("E5" . 8))
(n ("B4" . 8))
(n ("D5" . 8))
The key is A minor, the meter is 4/4 time, the tempo is mm=112. In the example, the first note is an E4 quarter note preceded by two rests. Performances can be stored using the same format. Standard MIDI files can be read and written to facilitate the exchange of music and performances with other programs. The resulting performance can be played via MIDI and/or displayed on different graphs, which show the music notation together with e. g. the relative deviation of duration.
The rules are written using rule-macros which contains a field for context specification. This allows for a sequential handling of each note in the score. The following is an example of the most common rule-macro each-note-if, which is used for most rules except the ensemble rules:
(defun <rulename> (<input parameters>)
(each-note-if
(<condition 1>)
(<condition 2>)
.
(<condition n>)
(then
(<action 1>)
(<action 2>)
.
(<action n>) )))
For the ensemble rules, rule-macros for parallel execution of the voices are used. These allow for context specification both horizontally, i. e. back and forth in the same voice, or vertically, i. e. using tones in other voices. Within a rule-macro the access functions are used to facilitate the access to the properties of the notes. Currently about 100 such access functions have been defined.
All these tools are added on top of the lisp environment, which means that all facilities in Common Lisp also are available. This has the advantage that it is easy to formulate an arbitrary rule. A disadvantage is that the rule specifications are not "clean" in the sense that a clear syntax can be defined. The following simple example of a performance rule looks for a phrase-start marker in the next note and, when found, it lengthens this note (the current note) by 40 ms:
(defun phrase ()
(each-note-if ;rule macro
(next 'phrase-start) ;context
(then ;then
(set-this 'dr (+ (this 'dr) 40)) ;action
)))
MIDI (Loy, 1985) is used as the communication between Director Musices and the synthesizer. It is a simple protocol combined with an interface specification. Originally it was intended to capture the playing on a synthesizer keyboard. It is remarkably standardized and used by all manufactures, which means that most synthesizers on the market can be directly used and interconnected. These advantages makes MIDI very attractive. Also it makes the program almost independent of the synthesizer, except for the following cases.
In a research application many problems occur. The first is that the coding of the parameters have weak relations to the physical sound measures. For example, sound level is not specified as such; instead it is given in terms of the key velocity measured in an arbitrary unit. We have compensated for this by measuring the sound level response of the synthesizers we used and defined a translation object in the program corresponding to each particular synthesizer. In this way the parameters can be specified in terms of normal physical measures, such as decibel. The synthesizer object can be specified in the score for each voice.
The second problem is that continuous changes of parameters during a
note's duration, such as sound level and fine tuning, affect all simultaneous
tones in the same MIDI channel. This is solved by using only one note per
MIDI channel. The MIDI volume is used for continuos sound level variation
and the MIDI pitch bend for continuos fine tuning.
Paper III contains a detailed presentation of the different parts of
the rule transformation from score to performance. Fig. III.1 illustrates
this transformation in terms of a block diagram.
Table 1. All performance rules.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The rules can be grouped according to the purposes which they apparently have in music communication. Two major principles can be identified: differentiation of categories and grouping (see e. g. Sundberg, 1993). Rules belonging to the former group appear to facilitate categorization of pitch and duration, whereas rules belonging to the latter group appear to facilitate grouping of notes. In the following, the rules are indexed according to these apparent purposes. Table 1 lists all current rules.
All rules are not intended to be used simultaneously. Some of the rules are partly overlapping, as explained below where each rule is discussed. The concept is that the user of the rules may act as a meta-performer where different performances can be realized by selecting rules and rule quantities. Our default value of the quantity has been K=1. This was developed when many rules were applied simultaneously. When fewer rules are applied higher quantities may be used.
A typical rule set is presented in Table 2 as an example of how the
rules can be used . For phrasing either PHRASE ARCH or HARMONIC CHARGE
combined with PHRASE FINAL NOTE can be chosen. The rules are listed in
the order of their application. This order is rather uncritical except
for AMPLITUDE SMOOTHING which must be applied after all rules affecting
sound level, and MELODIC SYNCHRONIZATION which must be applied after all
rules affecting duration.
Table 2. An example of how to combine some of the rules.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Next the rules listed in Table 1 will be discussed. Each rule is briefly
described, and its usage and limitations are discussed. The reference given
in the description section refers to the most complete description. Cases
of independent evidence in support of the rule are presented, wherever
applicable. Note however that most of the independent evidence was found
after the rule was first defined. Formal experiments carried out to test
generality and applicability of the various rules are described and commented
in the section Evaluation.
Description. This rule makes short notes shorter and softer (Paper I). The duration and loudness variation can be separated. The rules are then called SHORT SHORT and SHORT SOFT.
Affected sound parameters: duration and sound level
Usage and limitations. This rule can be used to model a number of different situations. It is most commonly used for its intended purpose, that is to shorten short notes. It can also be used negatively, i. e. to lengthen short notes instead. This might be called for because of the emotional character of the music, as shown by Gabrielsson (1995). The rule can also be used to account for notational conventions.
Independent evidence. Evidence for the SHORT SHORT principle was found by Taguti et al. (1994). They measured performances of the third movement of Mozart's Piano Sonata K. 545 and found that sections consisting of sixteenth notes were played at a higher tempo than sections consisting of eighth notes. Similarly, a listening panel preferred a performance with a tempo increase between 5 and 10 % for the sixteenth note sections. However, the rule will not give the intended result at the given tempo (mm=125) because the sixteenth notes are too short to be fully affected by the rule. This is probably due to a lack of similar music examples when the rule was developed and a modification of the rule definition may be made.
The same principle was found by Gabrielsson (1987) in the pattern dotted-eighth-sixteenth-eighth where the sixteenth note was in average shortened by 8 % of the nominal value. When the rule is applied with the default value K =1, the eighth notes are shortened by 5 %. A similar comparison with the amplitude variation in the same pattern is less clear. The sixteenth note is in about half the cases played more softly than both the preceding and the following note and in about 85% of the cases more softly than the following note.
A notational convention was found both in measurements by Sundberg et al. (1995) and by Bengtsson & Gabrielsson (1983). A dotted eighth note followed by a sixteenth note was always performed with much smaller duration ratio than the notated 3:1 ratio (see Fig. III.4).
Comments. A potential improvement could be to further differentiate between different contexts so that side effects such as unintended notes remained unaffected. For example, the 3:1 duration ratio might be considered in a separate rule, much in the manner the 2:1 duration ratio is addressed in DOUBLE DURATION.
Description. For two notes having the duration ratio 2:1, the short note will be lengthened and the long note shortened (Paper I).
Affected sound parameters: duration
Independent evidence. The principle was first found by Henderson
(1937) where he explained it as a consequence of phrasing and accent. It
was later found in many different music examples (Gabrielsson et al, 1983;
Gabrielsson, 1987).
Description. Accents are given to notes in the following contexts: (a) a short note between long notes, (b) the first of several short notes, and (c) the first long note after an accented note (Paper I).
Affected sound parameters: sound level envelope
Usage and limitations. This rule models accents performed on
instruments with a continuous sound where the sound level can be changed,
such as woodwinds, brass, voice. An alternative formulation, affecting
only the overall sound level of each note, has not been tried. However,
the ideas have been incorporated in PUNCTUATION.
Description. Pitch deviation from equal temperament is increased in proportion to pitch height (Paper I).
Affected sound parameters: pitch
Usage and limitations. This rule is intended to be applied primarily to a single voice. A combination of this rule and MIXED or MELODIC INTONATION may be possible, but has not been tested. In the current implementation in Director Musices, this is not provided for.
Independent evidence. Stretching has been observed both in direct matching of octaves and in measurements of performances (Sundberg & Lindqvist, 1973). The stretching in pianos is about 3-4 cent/octave for the two octaves above A4.
Comments. We observed during experimentation that upgoing intervals
were easily stretched but downgoing intervals were not. This could indicate
that a performer stretches only the upgoing intervals and has some other
method to keep the overall pitch the same during the piece. In upgoing
intervals the stretching can be increased to 6 cent per octave and the
value 4 cent, as given by the definition in Paper I, is a compromise. Another
possible improvement would be to make the stretching dependent on frequency
since this has been observed in experiments.
Description. This rule increases the loudness in proportion to the pitch height (Paper I).
Affected sound parameters: sound level
Usage and limitations. One of the purposes of this rule is to model the physical properties of some instruments. The sound level of voice, brass and some woodwinds increases with pitch when a musician is instructed to play at a constant dynamic level. For keyboards, strings and plucked instruments the sound level is not affected by the pitch in the same manner (Burghauser & Spelda, 1971).
Comments. According to Lars Frydén, the effect is often introduced on purpose even on the latter instruments. Also, the phrases are often composed so that the most important note of the phrase is also the note with the highest pitch. In this case an acceptable phrasing can be obtained using this rule only.
It is a simple but in our experience often a very efficient rule. However,
when several of the other rules are applied, it tends to be superfluous,
especially if macro-level rules are used.
¨Description. This rule accounts for the "remarkableness" of the tones in relation to the underlying harmony. Sound level, duration and vibrato extent are increased in proportion to the melodic charge value (Paper I).
Affected sound parameters: sound level, duration and vibrato extent
Usage and limitations. The rule is not applicable in atonal music. An analysis of harmony must be provided in the score.
Comments. Melodic and harmonic charge, as defined below, belong to the same category but are applied on different levels. The idea is to put emphasis on unusual events on the assumption that these events are less obvious, have more tension and are more unstable. The melodic charge value, Cmel (Paper I, p. 60) is defined as a value reflecting the note's distance on the circle of fifths to the root of the current underlying chord. The values of Cmel is largely a distance measure on the circle of fifths with the exception that there is more weight on the subdominant side.
Although melodic charge is not the same as tone proximity, Cmel correlates with the mean probe tone ratings to the major scale (r=0.86) found by Krumhansl & Kessler (1982). It also correlates with the frequency of occurrence of tones in Schubert themes (r=0.86) according to Knopoff & Hutchinson(1983), see Sundberg et al. (1989).
Note that melodic charge is not associated with any particular scale
since it is the same in both major and minor tonality. This can cause problems
when simultaneous harmony is played creating dissonant intervals. For example,
a major third is sounded in the melody at the same time as a C minor chord
is held below. This major third should be considered quite remarkable in
this context, but is not signaled by MELODIC CHARGE. This phenomenon should
be considered as a separate device which currently has not been addressed.
Description. The pitch deviation from equal temperament (ET) is made dependent on the note's relation to the root of the current chord. In principle, minor seconds are performed narrower than ET, e. g. the leading tone is higher than ET (Paper I). It is similar to Pythagorean tuning.
After the definition in Paper I, it has been redefined slightly as follows: The cent deviations in parentheses in Paper I will be applied for a given note when (1) it is preceded and succeeded by tones (i. e. not rests), (2) the previous tone is not a semitone below, and (3) the following tone is a semitone above.
Affected sound parameters: pitch
Usage and limitations. The resulting pitch deviation is in general opposite to how a interval is tuned so as to avoid beats (HARMONIC INTONATION or just intonation). Consequently, it is intended to be applied only to single voices. In polyphonic music MIXED INTONATION is more appropriate.
Independent evidence. The resulting pitch deviation was found
to correlate with the signed melodic charge value (Sundberg et al. 1989),
with violin intonation (Sundberg, 1993) and also with the intonation of
five out of ten singers performing Schubert's Ave Maria (Eric Prame, personal
communication)
Description. The melody can be divided into small musical gestures normally consisting of a few notes. This rule tries to identify and perform these gestures. It consists of two parts: the gesture analysis and the application of these in the performance. The gesture analysis is a complex system of 14 subrules where concepts from LEAP ARTICULATION and ACCENTS are used. The identified gestures are performed by inserting micropauses at the boundaries (Paper III).
Affected sound parameters: duration, offset to onset duration
Usage and limitations. The rule replaces LEAP ARTICULATION (MICROPAUSE)
and partly ACCENTS, although the application in the performance is different.
A preliminary evaluation by Frydén indicates that about 90% of the
inserted gesture boundaries are at an appropriate position.
Description. This rule inserts a dip in the level envelope between the notes in a melodic leap. The dip level is related to the size of the leap and to the duration of the notes (Paper I).
Affected sound parameters: sound level envelope
Usage and limitations. This rule applies to instruments with
a continuous sound where the sound level can be changed, e. g. woodwinds,
brass, voice.
Description. This rule inserts a micropause between the notes in a melodic leap. The length of the micropause is proportional to the magnitude of the leap (Paper I).
Affected sound parameters: offset to onset duration.
Usage and limitations. This is a simplified version of above
that only alters note durations. The concept of the rule is included and
complemented in PUNCTUATION and consequently less needed when PUNCTUATION
is applied. There is also a physical effect whereby on many instruments
it takes more time to move to a tone that is more physically remote. This
effect can be approximated by this rule, although it is dependent on the
specific instrument played and may be a rather complex function of the
fingering, for instance.
Description. The first note in an ascending melodic leap is shortened and the second note lengthened if the preceding and succeeding intervals are by step (less than a minor third). In a descending leap the first note is lengthened and the second shortened. The amount in ms is only dependent on the interval size of the leap (unaffected by the duration) (Paper I). Observe the erratum in the rule description.
Affected sound parameters: duration
Usage and limitations. This rule is typically effective in a
romantic context with rather long note values. It can not be used in conjunction
with MELODIC SYNCHRONIZATION in Director Musices since the generated sync
melody will contain new large leaps at the points when the sync melody
switches between the voices. A desirable improvement of this rule would
be to constrain its application, e. g. not to trigger at punctuation boundaries.
Description. The durations in an ascending melodic line are shortened (Paper I).
Affected sound parameters: duration
Usage and limitations. This rule makes the notes "aim"
towards the target note, that is, the top note. It is rather unselective
in that it shortens all notes preceded by a lower note and followed by
a higher note, rather than picking out an ascending line.
Description. The rule smoothes out the level differences between subsequent notes by changing the level envelope linearly from onset to onset (Paper I).
Affected sound parameters: sound level envelope
Usage and limitations. This rule is intended for instruments
with a continuous sound where the sound level can be changed, e. g. woodwinds,
brass, voice. It is essential for a realistic performance on these instruments.
Description. All eighth notes appearing on a strong beat will be lengthened and all eighth notes appearing on a weak beat will be shortened. This applies also to all notes or rests starting or ending at a weak position (Paper I).
Affected sound parameters: duration
Usage and limitations. This rule is used both in jazz (swing-feel) and in some early baroque music. In Director Musices no other note values than eighth notes in 4/4 time are implemented (eighth note 1, 3, 5 and 7 will be lengthened and eighth note 2, 4, 6 and 8 will be shortened).
Independent evidence. It is a well known effect, but rather few measurements has been made. One exception is Rose (1989) who measured eighth note durations in a jazz piece. He found a mean duration ratio of 2.38:1 between two consecutive eighth notes. At the given tempo (mm = 132) the preferred quantity of INÉGALES was found to be K = 1.8 (Paper III). This corresponds to a duration ratio of 2.33:1. See also the section about preference quantities below.
Notes inégales are mentioned in most books about interpretation
of early music. (e. g. Dart 1964; Ferguson, 1975). Recently an entire book
was dedicated to notes inégales and dotted notes (Hefling,
1993).
Description. The rule inserts a dip in the level envelope between the notes in a repetition. The dip level is related to the size of the leap and the duration of the notes (Paper I).
Affected sound parameters: sound level envelope
Usage and limitations. It is intended for instruments with a
continuous sound where the sound level can be changed, e. g. woodwinds,
brass, voice.
Description. A micropause is inserted between two notes of same pitch, without altering the interonset duration (Paper I).
Affected sound parameters: offset to onset duration
Usage and limitations. An alternative formulation of above for
instruments where the sound level envelope is not variable.
Description. Tempo curves in form of arches with an initial accelerando and a final ritardando are applied to the phrase structure as defined in the score. The sound level is coupled with the tempo variation so as to create crescendi and diminuendi. The way in which it affects the performance can be varied by several additional parameters, for example the hierarchical phrase-level, the amount of lengthening of the last note in each phrase, the position of the turning point (Paper III).
Affected sound parameters: sound level, duration
Usage and limitations. This rule is rather sensitive to musical style and personal taste. In romantic music the amount can be rather large while in Baroque music, for instance, it has to be much lower. There is a large variation seen in measurements of the same piece played by different performers or different pieces played by the same performer.
Independent evidence. The rule originated from measurements by Sundberg et al. (1995). The accelerando/ritardando shape has been observed in many previous measurements (e. g. Henderson, 1937; Gabrielsson, 1987; Shaffer & Todd, 1987; Repp 1992). Corresponding dynamic changes in terms of a crescendo/diminuendo shape are also often observed. However, these dynamic changes seem not to be directly coupled to the tempo changes.
Quadratic functions are used for the relative deviation as a function of nominal time (or score position) and were also found to fit well with the average of phrase ritardandi measured in Schumann's Träumerei by Repp (1992), as mentioned in Paper III. This shape is similar but not identical to the square-root function derived by Kronman & Sundberg (1987), using a simple model of stopping from running. One advantage of the quadratic function is that the derivative is zero at the beginning of the ritardando, i. e. it starts more smoothly, which possibly is more natural.
Comments. For a performer the conscious control of parameters that vary relatively slowly in time must be higher than the conscious control of fast events. It means that the macrolevel is more easily manipulated by the performer and that more individual variation may be seen. This may be reflected in this rule, as many additional input parameters were needed.
A desirable improvement would be to couple the different parameters
more to features in the music and to the desired character of the performance.
A separate model of the sound level would also be desirable, similar to
Todd's extension to his phrase model (Todd, 1992).
Description. This rule marks phrases on two hierarchical levels: phrase and subphrase. The last note in a phrase and the last note in the piece are lengthened. After the last note of a phrase or subphrase a micropause is inserted (Paper I).
Affected sound parameters: duration and offset to onset duration
Usage and limitations. It assumes that a phrase analysis is supplied in the score. In Director Musices the format for this phrase analysis and the one used by PHRASE ARCH are currently different.
Independent evidence. A lengthening of the last note only in a phrase can sometimes be found (see e. g. Henderson, 1937; Bengtsson & Gabrielsson 1983, p. 32)
Comments. One could argue that this marking of phrases is rather simple. This may be true if the rule is used in isolation. However, the other rules may help the marking of phrases implicitly. Of these, the most important is HARMONIC CHARGE since that rule uses the same context as phrases but in a different way.
This rule resembles speech, where the last syllable of a sentence is
lengthened. This effect is so articulated that if this lengthening is not
done, the last word sounds shortened, even though it has a normal duration
(Carlson et al, 1989).
Description. This rule marks the distance (related to the distance on the circle of fifths) of the current chord to the root of the current key. Sound level, duration and vibrato frequency are increased in proportion to the harmonic charge value. The increases and decreases of these parameters are gradual with linear interpolation between chord changes (Paper I).
Affected sound parameters: sound level, duration and vibrato frequency
Usage and limitations. This rule is not applicable in atonal music. An analysis of harmony must be provided in the score. It will generate a phrasing partly opposite to PHRASE ARCH. Consequently, HARMONIC CHARGE and PHRASE ARCH are not intended to be used simultaneously.
Independent evidence. The idea of marking the harmonic progression using dynamics is not new. Quantz (1752, TAB: XXIV) presented a music example with dynamic marks for each chord. This figure is also shown on the cover page. One principle found in the example was the marking of most dominant to local tonic chords with forte going to piano. The same local effect is obtained in HARMONIC CHARGE, although the total dynamic level will depend on the distance to the main tonic as well.
Harmonic charge is a function of a given chord's relation to the tonic, reflecting its tension. The harmonic charge is not the same as the proximity of chords within a tonal region which has been examined both theoretically (Lerdahl 1988, Longuet-Higgins 1987) and experimentally ( Krumhansl & Kessler, 1982). The proximity is more a measure of how easily a transition between different chords can be made. One example is the cadence V to I where the V has quite strong tension but is in close proximity to I. Nevertheless, the harmonic charge value correlates with the probe chord ratings by Krumhansl & Kessler (1982); see Sundberg et al. (1989).
Comments. In the case of a temporary new tonal region within a piece, the tonic in the analysis can stay the same since the rule in general works in the intended way in tonal regions close to the original tonic. This also has the advantage that the problem of treating the change of tonic in an overlap region is avoided.
One uncertain part of this rule is the chord analysis. In general this
can be done on several levels of detail and usually there are also chords
which can be analyzed in different ways. The level of the chord analysis
in this rule should be on structurally important chords with the exclusion
of passing chords. No tensions, such as dominant sevenths, are considered
at the moment.
Description. This rule increases the sound level and duration in areas where the intervals between the notes are small (Paper I).
Affected sound parameters: sound level and duration
Usage and limitations. This rule is intended to replace MELODIC CHARGE and HARMONIC CHARGE in atonal music, when the harmonic analysis can not be obtained.
Comments. Some evidence for the principle of this rule was found in an experiment by Krumhansl & al. (1987). They studied 12-tone serial music to see if a listener could perceive the structure of the 12-tone row. It was a probe tone experiment where first a context was presented consisting of various excerpts from a 12-tone row. After the context, one tone from the same row was played and the listener had to judge the similarity of this tone compared to the context. In the result, one group of listeners gave consistently very low ratings for tone repetition (when the last tone of the context was the same as the probe tone). This means that a repetition of notes was not expected at that point and considered as an unusual event. This is somewhat in accordance with chromatic charge where areas of pitches close together are considered remarkable and will be emphasized, although closeness in pitch is not the same as tone repetition.
An interesting experiment is to apply this rule to tonal music. In this
case it is usually not very successful, which in turn indicates that there
must exist some differences of principle between tonal and atonal music.
One explanation could be that in contemporary music the intervals are generally
large compared to those in traditional music. This means that in contemporary
music, areas with notes close together are rare and therefore can be emphasized
according to the principle "put emphasis on unusual events" which
is a important principle in the rule system and is applicable also to speech
(Carlson et al. 1987).
Description. The tempo at the end of the piece is decreased according to a square-root function of nominal time (or score position) (Paper I). Kronman and Sundberg (1987) developed this model as a simple physical system to describe the stopping from running. The parameters of the model were fitted to data of ritardandi measured by Sundberg & Verillo (1980)
Affected sound parameters: duration
Description. A new voice is constructed consisting of all new tone onsets from all voices. If several tones appear on the same onset, the one with the highest melodic charge value will be chosen. All duration rules are then applied to this new voice and the resulting timetable is transferred back to the original voices. This means that all simultaneous notes in all voices will be perfectly synchronized (Paper I, Sundberg et al., 1989). It is also called T2 in Paper II
Affected sound parameters: duration
Usage and limitations. This rule was originally intended to be used only in a polyphonic context where each voice can sometimes function as melody. However, our experience is that it works well in most situations including solo voice with accompaniment. One exception is complicated polyrhythmic figures when BAR SYNCHRONIZATION or a similar model may be more appropriate. The results of other rules can be altered. For example, it is not recommended to use it in combination with LEAP TONE DURATION since artificial leaps are created in the new voice which may not exist in the original voices.
Comments. A possible extension would be to introduce controlled
asynchrony. As many researchers have found, asynchrony is often used in
a consistent way, for example the melody or sometimes the lowest voice
is played earlier than the intermediate voices (see Gabrielsson, in press
for an overview)
Description. This rule synchronizes the onset times for the first note in each bar. The length of the voice with the most number of notes will be used as the bar length. The other voices will be adjusted proportionally to the same length (Paper I).
Affected sound parameters: duration
Usage and limitations. Intended to be used when the MELODIC SYNCHRONIZATION
is not appropriate, primarily in situations where complicated polyrhythmic
figures occur. A possible extension would be to synchronize on important
points in the music or at beat level.
Description. This rule is a combination of MELODIC and HARMONIC INTONATION, taking into consideration both the melodic strive to intonate minor seconds smaller than equal temperament and at the same time allow for beat-free chords. The initial pitch deviation will be set according to the melodic intonation. Slowly, the pitch deviation will change to a beat-free interval relative to the root of the chord (Paper I, Sundberg et al., 1989).
Affected sound parameters: pitch envelope
Usage and limitations. Intended to be used primarily in polyphonic
music.
Description. Every note is tuned so that the beats are minimized relative to the root of the current chord (Paper I).
Affected sound parameters: pitch
Usage and limitations. This rule is not intended to be a stand-alone
rule. It is used mainly for demonstrations of the effect of tuning each
chord so that beats are minimized. A melody will normally sound out of
tune. This is the target tuning for long chords in MIXED INTONATION.
The score used as input to the rules is basically clean from extra markings such as legato slurs, dots, dashes etc. The reason was that we wanted to explore how much of the associated expressive deviations can actually be automatically deduced from the musical context and described by means of a rule system. Also, performers often have the freedom to either to comply or disregard such signs (see e. g. Todd 1992). This is not to say that all such signs are superfluous; sometimes they would be used to mark effects which cannot be deduced from the musical context. It seems to be a complicated interaction between the notated articulation marks and the articulation induced from the notes themselves. This problem is currently not considered in the rule system. However, the score does contain extra symbols representing a phrase and a harmonic analysis.
One problem in using the score as input is that notation conventions differ between styles, composers and time periods. Historically, the notation has gradually changed from being rather sketchy to become more and more specific. For example, in Baroque music a dotted eight note followed by a sixteenth note was not supposed to be performed exactly as a 3:1 relation but rather indicated that the first note should be longer than the following note. In some contexts it would be performed to closer to 2:1, or in other contexts closer to a double-dot, because the notation of double-dotting was not used before the mid-18th century (Ferguson, 1975; Dart, 1964). DURATION CONTRAST achieves some of these effects, but new rules are needed for a more complete solution.
Furthermore, notational conventions exists that are style dependent. In jazz, two consecutive notes are often performed as an approximate 2:1 relation. In the literature, three different notations have been used for such note couples: (1) a dotted eighth note followed by a sixteenth note, (2) an eighth note triplet consisting of a quarter and an eighth note, or (3) two eighth notes. The last one is the most common today. The rule INÉGALES, which models this effect, assumes that this convention is used.
Summarizing, it does not seem possible to develop a universal performance
program which, using nothing but the score information as the input, produces
musically acceptable performances of input score files irrespective of
which notation conventions were applied. However, these problems should
not be overemphasized. The rule system works surprisingly well for a great
variety of music.
The marking of the meter with e. g. an accent on the first note in the bar, is deliberately not taken into account by the rules. Henderson (1937) failed to find such accents in piano performances. A better starting point is to use the melodic and rhythmic context of the music itself and let this determine the performance.
One complication of using the bar lines in a performance system is that in many cases the notated bar lines do not agree with the perceived meter. There are also many ambiguities in the music literature where the meter can be interpreted differently. This is not to say that the notated bar lines do not affect the performance (e. g. Sloboda, 1983). This is another example of the complicated interaction between the notated guide-lines and the performance discussed above.
Still the bar unit plays an important role in some types of music, often
because of the occurrence of a repetitive metrical pattern which coincides
with the bar. Music can be more or less melodically oriented (romantic
music etc.) or rhythmic oriented where metrical deviation patterns may
be called for (Bengtsson & Gabrielsson, 1983; Rose, 1989). The rule
system puts more emphasis on the melodic aspects in this sense. The only
rule that takes the bar into account is INÉGALES, disregarding melodical
context. Again, the interaction between the melodic and rhythmic features
may be rather complex as they often are in conflict.
Ideally, the rules should work for all tempi. An important question is whether the deviations from nominal durations should be calculated on a relative or an absolute basis; relative deviations imply that the perturbation is calculated in percent of the note's nominal duration, while absolute deviations mean that a fixed amount of milliseconds is added or subtracted. Strong arguments seem to favor relative deviations; for example, the note values in music notation is built on the principle of doubling and halving. On the other hand a perfectly strict application of the principle of perceptual lengthening does not seem realistic; for example, a percentual lengthening of a long note may add extra beats.
The absolute tempo is also important. For example, Desain & Honing (1994) showed that the expressive timing does not scale proportionally with tempo.
Most of the rules use either a fixed increase or a relative increase
in per cent of the note's duration. These simple transformations have been
surprisingly efficient and a compensation can easily be done manually by
adjusting the quantity K. The effect of absolute tempo has been considered
in DURATION CONTRAST. The rule is only dependent on the absolute durations
of the notes and only indirectly on the duration relations between notes,
see Fig. I.7 See also the section Swing factor as a function of tempo below.
Obviously our system is restricted to notated music. The emphasis has
been placed on Western classical music, but folk-melodies, lullabies, jazz
and contemporary atonal music have also been tried. Thus, there are indications
that many of the rule principles are in fact of a more general nature.
This aspect was pursued in Paper II, where the rules were successfully
applied to atonal music. The fact that some of the principles are found
also in speech and possibly also in body motion (see also the section Extramusical
sources....) indicates that the principles are similar for many types of
human perception/motor activity.
The quantity of each rule is not fixed; on each rules there is an input parameter K that can be used to alter the total amount of deviation caused by that rule. One can easily make different but still plausible performances by adjusting the K values. For PHRASE ARCH it was clearly not sufficient with one input parameter. The reason could be that this rule is more consciously controlled by the performer and also that it communicates many aspects of the music. It could also be that we have not yet found how the parameters are coupled.
In some rules the K value is used to control several output parameters.
For example the K value of MELODIC and HARMONIC CHARGE affects three parameters
simultaneously. Separate K values for each of these output parameters may
be an interesting possibility.
When many rules alter the same parameter of a given note, an interaction
problem occurs. This problem was solved by reducing rule quantities. Still,
sometimes unexpected results occur such that a rule for a local detail
influences a global parameter such as tempo. Improvements have been made
by using more complex and complete rules with a more specified context
so as to achieve an appropriate triggering. This means that in general
fewer rules are needed at the same time. The interaction effects of several
different principles have been integrated in PUNCTUATION.
Vibrato extent and vibrato frequency is altered by MELODIC and HARMONIC
CHARGE. However, to generate a realistic vibrato more rules are needed
(Prame, 1994). These rules seems to be quite dependent on the type of instrument
synthesized.
An overall goal in the development of the system has been generality,
i. e. to avoid instrument specific rules. For a complete synthesis, such
rules will have to be included.
The original purpose of Paper IV was to answer the following question: given that the duration of one note is changed by a rule, how large must the change be to be perceptible? As explained in Paper IV this question is not so simple. For a sequence of tones of equal duration > 250 ms the smallest perceptible deviation is about 5%. However, the length of the sequence and the duration are relevant factors; if the sequence is short (less than 10 tones) and the duration is < 250 ms, the absolute JND was found to be constant at about 10 ms. Thus, even for these relatively simple cases of constant duration and constant pitch, the JND values vary considerably for different types of perturbations and methods.
In a real music example at least the following additional factors may influence the JND: (1) perceptual tempo or beat rate, which is mentally extracted from the music (Parncutt, 1994); (2) note value variation (Monahan & Hirsh, 1990), (3) pitch variation (Monahan & Hirsh, 1990; van Noorden, 1975), and (4) phrase structure (Repp, 1994a).
As observed by Repp, a lengthening occurring in an expected location is harder to detect than if it appears in an unexpected place. A comparable effect can be experienced by listening to the examples on the CD-ROM where a rule is applied with negative quantities. The perceptual effect of such negative applications is mostly much greater than that of the positive application.
Another factor in real music is the option to focus the attention on
different aspects of the performance. Indeed, these difficulties provide
reasons to question the relevance of musical contexts in experiments attempting
to define JND values of general validity (cf. Sloboda, 1985). Nevertheless,
such JND values represent musically relevant information, e. g., telling
the performer what degree of finger movement accuracy is required. Also
such information is obviously needed in the development of a rule system
for music performance.
The smallest quantity of a rule that could be detected when comparing with the deadpan performance was investigated in Paper V, Exp. 1 and in Paper VI. Both investigations used short melodic excerpts but differed with respect to method, subjects and acoustic environment. These investigations showed that the JND for a small deviation in a real music example can be estimated, using deviation types that are closer to real performance variations than e. g. perturbation of a single tone in a melody. Comparing such JND values with preferred rule quantities is an interesting possibility.
In Paper V a method of constant stimuli was used with pairwise presentation of melody excerpts, deadpan and with the rule. The quantity of the rule was varied from zero to large. Since the time for the experiment was limited the same stimuli was only presented once or twice. The results could therefore only be presented as averages over all subjects rather than individual JNDs. One interesting finding was that the musicians had a significantly higher eagerness to answer that the two examples differed when they were identical.
These papers also investigated the relevance of musical experience. Paper V suggested a great difference between musicians and nonmusicians. In several cases the group of nonmusicians failed to detect even the maximum deviations. In Paper VI on the other hand, no difference associated with musical experience could be observed except for fine tuning. Musical experience seemed completely irrelevant to the responses for the three rules altering duration and for the rule altering mainly sound level. This was true even if the nonmusicians were compared only with the most experienced professional musicians.
Several reasons for this difference could be considered. The sound examples were longer in V (7-18 s compared to 3-6 s in VI). This could influence the comparison task. The short examples could be compared in short term memory. For the long examples a different strategy would be required. Longer examples also put higher demands on the ability to focus on specific details.
Another reason could be that the experiment described in Paper VI facilitated focusing and allowed more training time. The stimuli were presented several times and with an adaptive quantity so as to zoom in to each subjects personal JND value. A sudden drop in the JND values were sometimes observed, indicating a change of focus.
The acoustics of the rooms may also have influenced the results. In
Paper V, the room used for the test of the nonmusicians was more reverberant
than the room used for the musicians. More reverberation could be expected
to increase the JNDs, at least for pauses. In Paper VI a sound-proof room
was used with loudspeakers at a constant distance with a constant sound
level.
Although experimental conditions differed substantially between the experiments described in Papers V and VI, it is of course interesting to compare the results. An assumedly reasonable JND estimate was made of the responses in Paper V which could then be compared to the JNDs found in Paper VI.
JND values for Paper V were estimated from the LOGIT estimation curves shown in Figure V.6. The quantity corresponding to half of the percentage of "Same" answers received for K (Q) = 0 was chosen as an estimate of the JND. These KJND values were then translated to maximum spans, MSJND, of the deviations in duration etc., occurring in the specific excerpt. This procedure was also used in Paper VI. MS was defined as the difference between the largest and smallest deviation found in the example and would thus reflect the total variation within the excerpt. The resulting KJND values and the corresponding MSJND are presented in Table 3. When the rule affected several parameters, the one was chosen which seemed most plausible according to psychoacoustic measurements and informal experience. In many cases the values from the nonmusicians in Paper V failed to reach the 50% level of detection, so that no JNDs could be estimated.
The MS JND were chosen as the parameter of comparison and will be discussed next. Since the nonmusicians in Paper V apparently failed to detect the differences for many rules, only the musicians' results will be considered.
Different intonation rules appeared in the two tests and a huge
difference in the JNDs (8.8 and 42 cent) was obtained. This can be explained
by two factors: (1) In the melody used in HIGH SHARP, there are two consecutive
salient octave jumps at the end, presumably simplifying the task. In the
melody used in MELODIC INTONATION, the interval with the largest deviation
was a tritone, the fine tuning of which was probably much harder to detect.
(2) The musicians in Paper V were mostly string musicians, thus particularly
trained in intonation.
Table 3. Overview of JND values from Paper V, Exp. 1 and Paper VI expressed in terms of KJND and MSJND of the affected parameters.
|
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
||||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
||||||
|
|
|
|
|||||
|
|
|
|
|||||
The deviations in duration were expressed in percent of the tone's duration, as most of the tones in these excerpts were rather long. According to the results from Paper IV the relative JND is approximately constant for tones of these durations. SHORT SHORT was tested in both experiments. Despite different excerpts and different rule formulations the MSJND values were quite similar (5.6 and 4.7%). MSJND for the other three duration rules were all higher, but in the same range (22.1, 17.2 and 20.2 %). These higher values can be explained by context; these rules are all of a local nature and in most cases they only produce displacements of the onsets of tones appearing in relatively weak metrical positions. SHORT SHORT, on the other hand, perturbs also the local tempo which may be easier to detect. This is in accordance with psychoacoustic measurements where the JND for tempo can be as low as 1% and the JND for displacement of one tone is about 5% (Paper IV).
Similar values were found for the MSJND for sound level in two rules (1.6 and 1.4 dB) and a higher value (4.6 dB) for CHROMATIC CHARGE. The higher value may reflect the much greater complexity of the atonal music excerpt used in this case.
MSJND for pause duration is harder to analyze since it is dependent on the acoustics of the listening room and also of the envelope characteristics of the sound. For PHRASE FINAL NOTE tone duration might be used for the detection as suggested by the reasoning above. The JND value 1.9 % is rather small but it is measured for a half note in the melody while the beat is quarter notes. This means that the beat rate perturbation is twice as high, or 3.8 % which may be possible to detect since it affects the local tempo.
Summarizing, the different JNDs are surprisingly consistent when the simple measure of the maximum span MS is used. In most cases the MS JND values also show a simple relation, a factor of 3 to 4, to the classical psychophysical JND values listed in Paper VI. That the values are higher is not surprising, taking into account the significant effects of complexity and expectation as demonstrated in previous research. Presumably these observations are valid only for the relatively long note values and medium tempi that were used in these examples; Paper IV indicated a different, more complex, behavior for shorter durations which may be reflected also in more musical contexts.
The combined results from all our JND measurements for duration supports
the idea of a perceptual model consisting of a flexible clock at the beat-rate
with pattern recognition for intermediate tones (see e.g. Shaffer 1981).
When the beat-rate is disturbed (i. e. the local tempo), the JND corresponds
to the psychoacoustic JND for tempo, as summarized in Paper IV. When local
durations are changed within a beat, keeping the beat rate undisturbed,
the JND corresponds to the psychoacoustic JND for single note displacement
and cyclic displacement, as summarized in Paper IV.
The evaluation by listening tests puts high demands on both the exact
formulation of the rule and the rule quantity. For example, if a rule induces
a lengthening of one single tone which must not be lengthened, some listeners
are likely to react negatively, rejecting the rule entirely, even if all
other applications of the rule in the same excerpts are musically correct.
Also the rule quantity is an important factor. If a rule is applied with
an exaggerated quantity, many listeners tend to prefer a deadpan version
in a comparison, even if the rule is musically correct. This problem has
been accounted for in the preference tests. The principles of the
rules are best evaluated either with the method of occurrence or with the
method of matching as described below.
Early versions of the rules were tested by Thompson et al. (1989) and Frydén et al. (1988). For a summary, see Sundberg et al. (1991). One major problem with these tests was that the rule quantities were quite small producing barely perceptible effects. However, many of the rules were shown to have a positive effect on the performance, in particular when several rules were applied at the same time.
PHRASE FINAL NOTE was evaluated in a listening test by Friberg et al. (1987). Four versions of two melodies were presented pair-wise always with K=1 as one the alternatives. In 70% of the cases the 15 subjects found the rule version the most musical. Another finding was that the subphrase and phrase markers could not be shifted.
The ensemble rules for intonation and synchronization were checked in a listening test (Sundberg et al., 1989). In the intonation part, two fixed tunings, just and equally tempered (ET), and early versions of MELODIC INTONATION and MIXED INTONATION were compared. The objective was to see if our model of ensemble intonation, namely MIXED INTONATION, would be favored by the listening panel. Three different polyphonic music excerpts were used, each exhibiting different intonation conditions. Much to our surprise, the ET tuning were rated highest on the average, with MIXED INTONATION as number two. It seems that ET serves as a reference which always produced acceptable results and that alternative tunings must be exactly "right" on every note to be accepted. This led us to a reformulation of MIXED INTONATION eliminating its apparent weaknesses. This new version was presented in Paper I, but has not been subjected to a listening test.
Two different synchronization methods were tested: MELODIC SYNCHRONIZATION
and BAR SYNCHRONIZATION. The subjects were asked to rate the quality of
the performances "with regard to ensemble playing, i. e., how simultaneously
the musicians played" in the synthesized examples. As expected, the
MELODIC SYNCHRONIZATION was rated highest. BAR SYNCHRONIZATION seemed a
possible strategy only in excerpts where only minor deviations occurred.
The applicability of the rules in an atonal context was tried in Paper II. Music examples were selected that represented various styles of contemporary, atonal music. Three piano excerpts and four random generated melodies were chosen. Initially different existing rules were tested on this new context. For obvious reasons HARMONIC and MELODIC CHARGE could not been used, which created a lack of long-term variations (at that time only HARMONIC CHARGE made these). Such variations were re-introduced by the new rule CHROMATIC CHARGE. The principle was to emphasize areas with shorter pitch distance, on the chromatic scale, between successive tones. An exact description is found in Paper I. This idea, introduced by Frydén, turned out to work very well in practice, although the reason why it works is still rather obscure. This is a striking demonstration of the advantage of the expertise constellation in our research team; here, Frydén's musical intuition came up with something that would have been difficult to find by means of a conventional investigation.
The quantities of the selected rules were fine-tuned for each excerpt.
In the subsequent listening test these performances were compared with
deadpan versions. As seen in Fig. II.1 there were almost total agreement
among the subjects that the versions with the rules sounded better than
the deadpan versions. An interesting finding was that this preference was
even more pronounced for the random generated melodies. This may indicate
that the need for performance rules marking the inherent structure in the
music is higher when the structure is harder to perceive by itself.
In the first implementation of the rules all quantities were fixed. However, it soon became evident that a variable controlling the overall quantity of a rule was needed. This was also supported by the results from investigations which showed that the amount of deviations suggested by Frydén was not perceptible to all subjects in the listening experiments. Therefore, a general quantity variable, K (originally Q), was introduced in all rules, whenever possible.
In Paper V, Exp. 2, a different evaluation strategy was used where professional musicians were asked to adjust K to their preferred values. In this way two questions could be answered: (1) Is there a general agreement among musicians that the rule improves the performance? and (2) What K values are preferred and how much do these preferred values vary among musicians?
The average K values and the corresponding confidence intervals are shown in Fig. V.9. According to a t-test four out of six rules were approved by the subjects. The excerpt used for DURATION CONTRAST, which was not approved, contained a duration ratio of 2:1 a context in which DOUBLE DURATION induces the opposite effect. This seemed to be the reason why it was rejected. This caused us to reformulate DURATION CONTRAST, such that it excluded the 2:1 case. The rejection of MELODIC CHARGE was due to one subject and may have happened by mistake, see Fig 3, below. By excluding this subject, the average preferred quantity was significantly larger than zero.
Again, a reanalysis of the data turned out to be interesting; Fig. 3, shows the individual K values for each subject and rule.
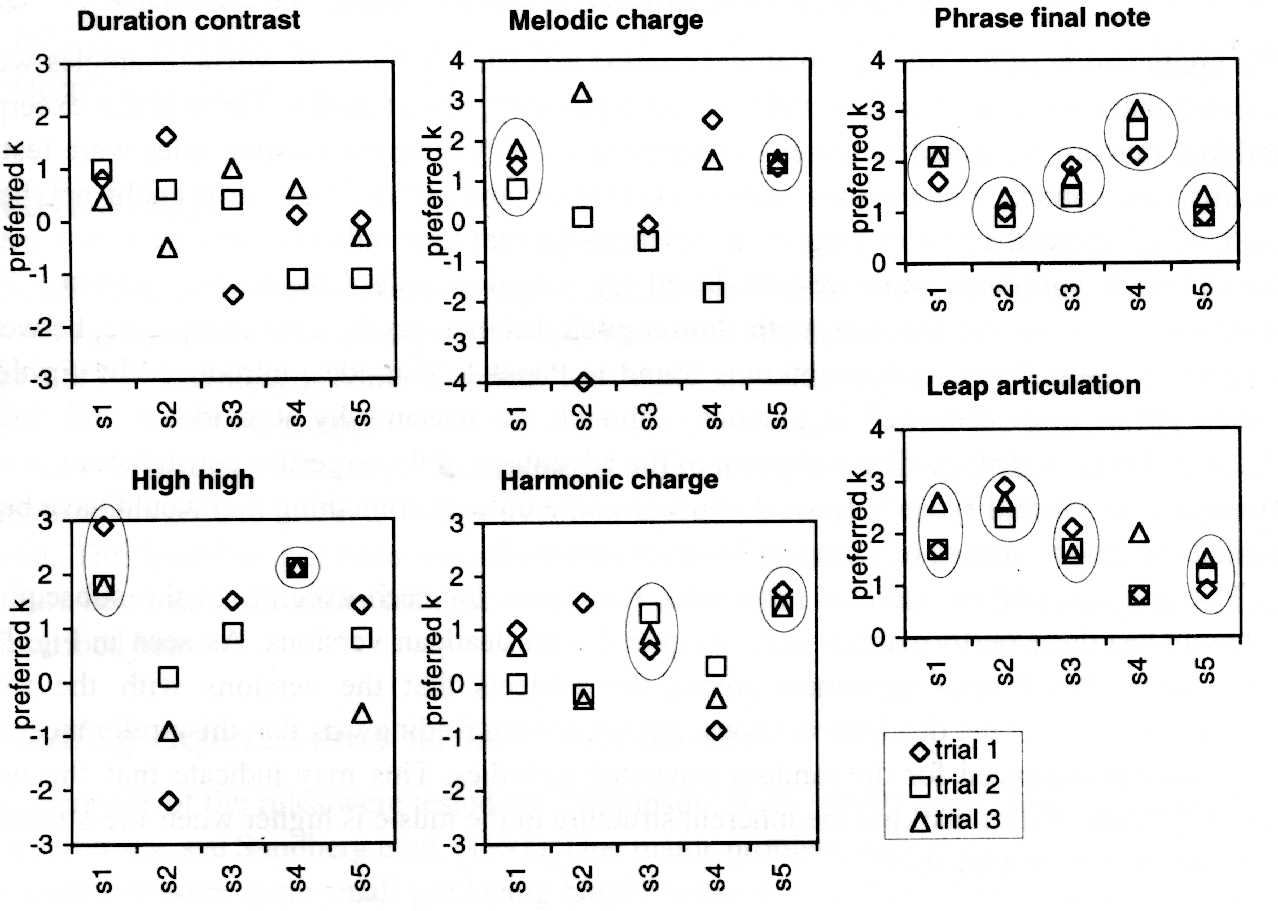
Fig. 3. The preferred K values for each subject and rule in Paper V,
Exp. 2. The circles marks the cases where a significant preference for
the rule was observed.
The rules showing the most consistent results are PHRASE FINAL NOTE (GMA 1 in Fig. V.9) and LEAP ARTICULATION (GMI 1A', in Fig. V.9, wrongly labeled GMI 1B). In these two rules, all subjects had a small intrasubject variation indicating that the task was simple and that the subjects knew from the beginning which quantity they preferred. A high intersubject variation indicates that the subjects disagree with regard to preferred K value. This variation was at most a factor of 2.5 (PHRASE FINAL NOTE, subjects 4 and 5). The task was probably facilitated by the fact that only positive values were used for these rules.
The remaining rules showed a less clear picture; these rules were clearly approved by some subjects, disapproved by few subjects, and displaying a relatively high variation for the other subjects. The variations can have many different reasons, such as rule conflict as for DURATION CONTRAST, problems to understand the deviations occurring when the quantity varies, or even mistakes. A fascinating case is subject 4 in HIGH HIGH. This subject adjusted to exactly the same value all three times, even exceeding the precision of the equipment which was about 1.5 cent. A t-test of the individual means yielded a significant positive quantity for the encircled points in Fig. 3. This is a rather strict test as only three values were averaged and e. g. only one mistake would have made the mean nonsignificant.
The average over subjects of these significant individual means were
used to estimate the average preferred quantity, given in Table 4. These
average K values better reflect which values those subjects preferred who
clearly approved the rule. As seen in the table, the K values are less
spread than in Fig. V.9 and are slightly higher than our default value
of K=1. This is not surprising since the default values were set when all
the rules were simultaneously applied. It is also possible that our long
term acquaintance with these rules facilitates the detection of deviations,
and this may lower our preference values.
Table 4. Preference quantities averaged over those subjects who clearly
approved of the rule. The corresponding maximum span MS of the affected
physical parameters in the given music excerpt are also presented. Data
from Paper V, Exp. 2. The MSJND are averages of the corresponding
data shown in Table 3.
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Since the maximum span MS of the physical parameters turned out to be useful measure of the deviations produced by a rule, these spans are also presented in Table 4. Most of the MS values are higher than the corresponding MSJND values. Hence at the average preference level, all parameters affected by a specific rule may be detected. The exception is MELODIC CHARGE in which all parameters seem to be close to their corresponding MSJND. This is different from the result in Paper V where the preferred deviations were found to be close to the musicians' JNDs.
In conclusion, all rules except DURATION CONTRAST (for obvious reasons) were clearly approved by at least two subjects. The preferred quantity was found to differ by a factor > 2 among the subjects.
In paper III, the quantity K for INÉGALES, i. e., the swing factor
in jazz, was adjusted for different tempi by 34 subjects. The excerpt was
a short jazz example, played on electric organ, bass and drums on a sample
synthesizer. The swing factor was found to vary almost linearly as a function
of tempo; large swing factors in slow tempi and small in fast tempi (Fig.
III.5). A K=1 corresponds to a 22% lengthening of the first note and a
shortening of the following note by the same amount (Paper I). This corresponds
to a factor 1.56:1 between two successive eighth notes. Some of the subjects
(including the author) preferred a more constant ratio irrespective of
the tempo, indicating individual preference differences. Interestingly,
the mean ratio at mm = 132 obtained by interpolation in Fig. III.5 was
2.33:1. This is very similar to the value of 2.38:1 found at this tempo
by Rose (1989) in a study of jazz performance.
The principles of the rules can in several cases be observed in measurements
of real performances. For each rule such cases have been presented in the
section Rules above. However, suggestive evidence was found more often
than cases of exact correspondence. If a given rule is not found in measurements
does not necessarily mean that it is invalid; several rules of this type
have been approved in listening experiments. For example, there are several
ways to signal emphasis on a single note. A performer may choose one of
these and disregard the others. This means that of all means that are available
to a performer, all are not used.
Another method is to match the quantities of the rules to a given performance. A rule-generated performance is compared to a measured performance. The rule quantities are adjusted so that the difference between the two performances is minimized. If a given rule was found to decrease this difference, there is evidence that this rule was used in that performance. How much of the variation that is explained by the rule can also be estimated. Using simple solving algorithms, several rules can be fitted simultaneously. This is close to multiple regression analysis, but with an increased flexibility. An advantage is that a given rule estimate can be subtracted from the measured performance. The residual may give further ideas of the remaining variation. An advantage compared to listening experiments is that many more rules and music examples can be tested.
An initial attempt to use this method is reported in Paper III, where
PHRASE ARCH and DURATION CONTRAST was fitted to two sung performances,
see Fig. III.4 Similar parameter matchings have been used by Todd (1985,
1989, 1992) for developing models for tempo and dynamics. Although rather
limited experiments, the method looks promising and will be used more in
the future.
An interesting question that has been less examined in previous research is why the expressive deviations are manifested in one particular way and not in another. It seems natural to assume that some of the specific behavior of these deviations originate from speech. This idea was developed by Carlson et al. (1989) who compared our musical performance rules with rules used in speech synthesis. Another plausible origin is our experience of physical motion of our body, a possibility explored in Paper VII.
A few related works about motion in music should be mentioned here in addition to those commented on in Paper VII. A selective overview can be found in Repp (1994b) who discusses the earlier, more intuitive, though thorough earlier work by Truslit and others and compares it with more recent contributions, mainly by Manfred Clynes and Neil Todd. An thought provoking idea advocated by Todd (1993) is that the vestibular system is activated during music listening and directly induces a sensation of self-movement, an idea which may or may not involve the experience of physical motion of our body.
In motion the idea of using Newton's laws, assuming a constant acceleration force, and the translating of this to tempo, was explored by Kronman & Sundberg (1987). Their results were implemented as FINAL RITARD. This idea was further elaborated by Todd (1992) to make a model of the accelerando/ritardando and crescendo/diminuendo patterns often used for phrasing. Despite the rather unnatural assumption of a step-wise change of the acceleration, these models were rather successful in predicting measured performances. It remains to be shown if and under what conditions a constant acceleration force is applied in real motion. It would also be interesting to find out if the modeled performance are capable of eliciting a sensation of motion in a listener. A more complete test would be to take some representation of real physical motion, translate it to music and check if it induces motion in listeners. This was attempted in Paper VII.
The transformation of motion to music was investigated by asking three different questions: (1) Does the force envelope for the foot during walking or running reflect some aspects of the motion sensation of the body ? (2) Can these force envelopes, translated to sound level envelopes, evoke an auditory sensation of motion? (3) Can different types of physical motion induce perception of different motion characters, if force envelopes are translated to sound level envelopes?
The vertical force envelope for the foot turned out to somehow reflect the type of walking and dancing. In running, on the other hand, much less difference could be observed. Six envelopes from walking and dancing were selected which had clearly differing envelope characteristics. Sequences of four isochronous tones with the same pitch were presented at different tempi to students of rhythm pedagogy.
In Exp. 1 subjects were asked to describe in their own words the character of the sound they heard and the number of motion words used were counted. Motion words were most frequent when (1) the intertone interval was close to 600 ms (upper Fig. VII.5), (2) the patterns were presented at the original tempo (Fig. VII.6), and (3) when humps in the envelope formed musically common patterns with the following tone envelope (Fig. VII.9).
In Exp. 2 the subjects were asked to describe what type of motion, if any, they perceived from the same sound sequences. Only the number of blank responses were analyzed. Despite the rather uncertain method, a few interesting observations could be made. The occurrence of blank responses in Exp. 2 confirmed the effect of absolute tempo; the blanks were more frequent for the slower tempi than for the fast (Table VII.II). The effect of the original tempo was also confirmed by the lower number of blanks for these presentations.
Exp. 1 and 2 indicated that motion could sometimes be induced by these sound envelopes and that there was an interaction effect between shape and tempo.
In Exp. 3 the subjects were asked to characterize the type of motion perceived along 24 motion adjective scales. Since according to Exp. 1 and 2 the original tempo was important for inducing motion quality only these examples were analyzed. In the factor analysis about half of the variance was explained by the first factor relating mainly to the tempo (Factor 1, Swift-Solemn). This is also reflected in Fig. VII.7 where the factor loadings for Factor 1 are plotted as a function of the tempo for the different gaits. All the factor loadings for the different gaits are plotted in Fig. VII.8. Different shapes occur even when the tempo is very similar. This indicates that also the type of motion can be transferred with this method. In some cases the judgment of the sound also corresponded to the intended intuitive character of the walking or dancing.
This investigation should be considered as a first attempt to directly
transfer physical motion to musical motion. Although rather limited methods
and statistic analysis were used, the results clearly indicated a possible
connection. This was despite the rather arbitrary choice of the parameters
that were transformed. The body motion has many degrees of freedom and
a better choice of parameters may reveal much stronger relations. This
also suggests that the actual connection between physical and musical motion
may be quite strong since it survives a rather arbitrary transformation.
In a future replication of this investigation, a visual test assessing
the physical motion quality would be valuable.
I first of all would like to thank Lars Frydén and Johan Sundberg.
Their importance for this work can not be overestimated. They began the
work and developed many of the current rules and ideas before I started.
They provided a wonderful creative atmosphere in our continuing team-work.
I would like to thank all colleagues at the lab for all help and especially
my room-mates, Gunilla and Sten, for coping with all the noise and bad
performances heard over the years. Many valuable suggestions was given
by Eric Prame and Anders Askenfelt who read the manuscript. I am also grateful
for the patience showed by my family, Elly and Jonathan, particularly during
the last weeks of the preparation of the manuscript.
Battel, G., U., & Bresin, R. (1994). Analysis by synthesis in piano performance: a study on the theme of the Brahms' "Variations on a theme of Paganini". in A. Friberg et al. (eds.), Proceedings of the Stockholm Music Acoustics Conference 1993, 69-73.
Bengtsson, I. & Gabrielsson, A. (1983). Analysis and synthesis of musical rhythm. in J. Sundberg, (ed.), Studies of Music Performance, Stockholm: Royal Swedish Academy of Music, Publication No. 39, 27-60.
Berndtsson, G. (1995). Systems for synthesising singing and for enhancing the acoustics of music rooms. Two aspects of shaping musical sounds, doctoral dissertation, KTH, Stockholm
Bresin, R. & Vecchio, C. (1994). Analysis and synthesis of the performing action of a real pianist by means of artificial neural networks. in I. Deliège (ed.), Proceedings of 3rd International Conference for Music Perception and Cognition, Liège 1994, 353-354.
Bresin, R. (1993). MELODIA: a program for performance rules testing, teaching, and piano scores performing. in Proceedings of the X Italian Colloqium on Music Informatics (CIM), AIMI, Padova.
Bresin, R. (1994). Performance of Musical Scores by Means of Neural Networks. in J. Sundberg (ed.), Proceedings of the Aarhus symposium on Generative grammars for music performance 1994 3-6.
Bresin, R., De Poli, G. & Ghetta, R. (forthcoming). A Fuzzy Formulation of KTH Performance Rule System. Proceedings of the 2nd International Conference on Acoustics and Musical Research 1995.
Burghauser, J., ùSpelda, A. (1971). Akustische grundlagen des orchestrierens, Regensburg: Gustav Bosse Verlag.
Carlson, R., Friberg, A., Frydén, L., Granström, B. and Sundberg, J. (1989). Speech and music performance: parallels and contrasts. Contemporary Music Review 4, pp.389-402.
Carlson, R., Granström, B. (1975). A phonetically oriented programming language for rule description of speech. in G. Fant, (ed.), Speech communication 2, Stockholm: Almquist & Wiksell, pp.245-253.
Clarke, E., F. (1988). Generative principles in music performance. in J. Sloboda, (ed.), Generative processes in music, Oxford: Claredon press, 1-26.
Dart, T. (1964). Musikalisk praxis: från senmedeltid till Wienklassicism (The Interpretation of music), Stockholm: Natur och kultur
Desain, P. & Hooning, H. (1994). Does expressive timing in music performance scale proportionally with tempo?. in Psychological Research 56, 285-292.
Ferguson, H. (1975). Keyboard Interpretation, New York & London: Oxford University Press
Friberg, A., Sundberg, J. & Frydén, L. (1987). How to terminate a phrase. An analysis-by-synthesis experiment on the perceptual aspect of music performance. in A. Gabrielsson (ed.), Action and Perception in Rhythm and Music, Stockholm: Royal Swedish Academy of Music, Publication No. 55, 49-55.
Frydén, L., Sundberg, J. & Askenfelt, A. (1988). Perception aspects of a rule system for converting melodies from musical notation into sound. Archives of Acoustics 13 (3-4), 269-278.
Gabrielsson, A. (1985). Interplay between analysis and synthesis in studies of music performance and music experience. Music Perception 3, 59-86.
Gabrielsson, A. (1987). Once again: the theme from Mozart's piano sonata in A major (K. 331). A comparison of five performances. in A. Gabrielsson (ed.), Action and Perception in Rhythm and Music, Stockholm: Royal Swedish Academy of Music, Publication No. 55, 81-103.
Gabrielsson, A. (1995). Expressive Intention and Performance. in R. Steinberg, (ed.), Music and the Mind Machine, Berlin: Springer-Verlag, 35-47.
Gabrielsson, A. (in press). Music Performance. in D. Deutsch (ed.), The Psychology of Music (2nd ed.), New York: Academic press.
Gabrielsson, A., Bengtsson, I. & Gabrielsson, B. (1983). Performance of musical rhythm in 3/4 and 6/8 meter. Scand J Psychol 24, 193-213.
Hansson, J. (1994). En C-version av musikprogrammet Rulle. Unpublished master thesis at KTH, Stockholm
Hefling, S., E. (1993). Rhythmic alteration in Seventeenth- and Eighteenth-Century Music: Notes inégales and overdotting. New York: Schirmer Books.
Henderson, A., T. (1937). Rhythmic organization in artistic piano performance. in C. E.. Seashore (ed.), Objective analysis of musical performance. Univ. of Iowa Studies in the Psychology of Music, Vol IV, Iowa City: University of Iowa, 281-305.
Hooning, H. (1990). POCO: An environment for analysing, modifying, and generating expression in music. in Proceedings of International Computer Music Conference 1990, 364-368.
Katayose, H. & Inokuchi, S. (1993). Learning Performance Rules in a Music Interpretation System. Computer and the Humanities, 27, 31-40
Knopoff, L. & Hutchinson, W. (1983). Entropy as a measure of style: The influence of sample length. Journal of Music Theory 27, 75-97.
Kronman, U. & Sundberg, J. (1987). Is the musical ritard an allusion to physical motion?. in A. Gabrielsson (ed.), Action and Perception in Rhythm and Music, Stockholm: Royal Swedish Academy of Music, Publication No. 55, 57-68.
Krumhansl, C. L. & Kessler, E. J. (1982). Tracing the dynamic changes in perceived tonal organization in spatial representation of musical keys. Psychological Review 89, 334-368.
Krumhansl, C. L., Sandell, G. J. & Sergeant, D. C. (1987). Tone Hierarchies and Mirror Forms in Serial Music. Music Perception 5, 31-78.
Lerdahl, F. (1988). Tonal Pitch Space. Music Perception, 5, 315-350.
Longuet-Higgins, H., C. (1987). Mental processes: Studies in cognitive science, Cambridge, MA: The MIT Press.
Loy, G. (1985). Musicians make a standard: The MIDI phenomenon. Computer Music Journal, 9 (4), 8-26.
Mazzola, g. & Zahorka, O. (1994). The RUBATO Performance Workstation on NEXTSTEP. in Proceedings of International Computer Music Conference 1994, 102-108.
Monahan, C., B. and Hirsh, I., J. (1990). Studies in auditory timing: 2. Rhythm patterns. Perception and Psychophysics 47 (3), 227-242
Palmer, C. (1989). Mapping Musical Thought to Musical Performance. Journal of Experimental Psychology: Human Perception and Performance, 15 (12), 331-346.
Parncutt, R. (1994). A Perceptual Model of Pulse Salience and Metrical Accent in Musical Rhythms. Music Perception, 11 (4), 409-464.
Prame, E. (1994). "Measurements of the vibrato rate of ten singers", J. Acoust. Soc. Am. 96 (4), 1979-1984.
Quantz, J., J. (1752,1926). Versuch einer anweisung die flöte traversiere zu spielen, Liepzig: C. F. Kahnt.
Repp, B., K. (1992). Diversity and commonality in music performance: An analysis of timing microstructure in Schumann's "Träumerie". J. Acoust. Soc. Am. 92 (5), 2546-2568.
Repp, B., K. (1994a). Detectability of rhythmic perturbations in musical contexts: effects of metrical structure and of musical experience. in I. Deliège (ed), Proceedings of 3rd International Conference for Music Perception and Cognition, Liège 1994 , 405-406.
Repp, B., K. (1994b). Musical motion: Some historical and contemporary perspectives. in A. Friberg et al. (eds.), Proceedings of the Stockholm Music Acoustics Conference 1993, 128-135.
Rose, R., F. (1989). An analysis of timing in jazz rhythm section performances. Dissertation abstracts international, 50, 3509A-3510A.
Shaffer, L. & Todd, N., P., McA. (1987). The interpretive component in musical performance. in A. Gabrielsson (ed.), Action and Perception in Rhythm and Music, Stockholm: Royal Swedish Academy of Music, Publication No. 55, 139-152.
Shaffer, L. (1981). Performances of Chopin, Bach and Bartok: studies in motor programming. Cognitive Psychology 13, 326-276.
Shultz, M. (1994). A Model of Musical Expression using Neural Networks with Rulebase Nodes. in J. Sundberg (ed.), Proceedings of the Aarhus symposium on Generative grammars for music performance1994 21-24.
Sloboda, J., A. (1983). The communication of musical metre in piano performance. Quarterly Journal of Experimental Psychology 35, 377-396.
Sloboda, J., A. (1985). The musical mind: The cognitive psychology of music, Oxford: Claredon press.
Sundberg, J. & Lindqvist, J. (1973). Musical octaves and pitch. J. Acoust. Soc. Am. 54 (4), 922-929.
Sundberg, J. & Verrillo, V. (1980). On the anatomy of the ritard: A study of timing in music. J Acoust Soc Amer 68, 772-779.
Sundberg, J. (1993). How can music be expressive?. Speech Communication 13, 239-253.
Sundberg, J., Frydén, L. & Askenfelt, A. (1983a). What tells you the player is musical? An analysis-by-synthesis study of music performance.in J. Sundberg, (ed.), Studies of Music Performance, Publication issued by the Royal Swedish Academy of Music Nr. 39, Stockholm, 61-75.
Sundberg, J., Askenfelt, A. and Frydén, L. (1983b). Musical performance: A synthesis-by-rule approach. Computer Music Journal, 7, 37-43.
Sundberg, J., Friberg, A. & Frydén, L. (1989). Rules for automated performance of ensemble music. Contemporary Music Review, 3, 89-109.
Sundberg, J., Friberg, A. & Frydén, L. (1991). Common Secrets of Musicians and Listeners - An analysis-by-synthesis Study of Musical Performance. in P. Howell, R. West & I. Cross (eds.), Representing Musical Structure, London: Academic press.
Sundberg, J., Iwarsson, J., L. & Hagegård, H. (1995). A singer's expression of emotions in sung performance. in O. Fujimura & M. Hirano (eds.), Vocal Fold Physiology: voice quality control, San Diego: Singular publishing group.
Taguti, T., Mori, S. & Suga, S. (1994). Stepwise change in the physical speed of music rendered in tempo. in I. Deliège (ed.), Proceedings of 3rd International Conference for Music Perception and Cognition, Liège 1994, 341-342.
Thompson, W. F.,Sundberg, J., Friberg, A., and Frydén, L. (1989). The Use of Rules for Expression in the Performance of Melodies. Psychol. of Music 17, 63-82.
Todd, N., P., McA. (1985). A model of expressive timing in tonal music. Music Perception 3, 33-58.
Todd, N., P., McA. (1989). A computational model of rubato. Contemporary Music Review 3, 69-88.
Todd, N., P., McA. (1992). The dynamics of dynamics: A model of musical expression. J. Acoust. Soc. Am. 91 (6), 3540-3550.
Todd, N., P., McA. (1993). Vestibular Feedback in Musical Performance: Response to Somatosensory Feedback in Musical Performance. Music Perception 10 (3), 379-282.
van Noorden, L., P., A., S. (1975). Temporal coherence in the perception of tone sequences Eindhoven: Institute for Perception Research.
van Oosten, P. (1993). Critical study of Sundberg's rules for expression in the performance of melodies. Contemporary Music Review 9(1-2), 267-274
Widmer, G. (1994). Learning Expression at Multiple Structural Levels.
in Proceeding of the 1994 International Computer Music Conference,
95-101.
Paper I, p. 59, the formulas should be:
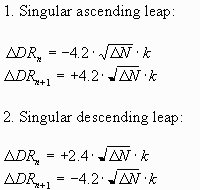
Paper V, p. 77:
Vibrato frequency was not used
p. 78:
"Leap articulation" should be "Leap duration"
p. 80:
"Durational contrast" should be "Short short"
"Leap articulation" should be "Leap duration"
On the CD-ROM the sound examples of the rules are stored as CD sound
tracks, i.e they can be played on a normal CD player. The following is
a list of all the sound examples with the corresponding track number. Within
each track the same example is presented with the rule quantities in the
listed order.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|||
|
|
|
|||
The following is a list of what the different authors did in each paper.
Paper II.
Friberg, A., Frydén, L., Bodin, L.-G., and Sundberg, J. (1991). Performance Rules for Computer-Controlled Contemporary Keyboard Music. Computer Music Journal, 15 (2), 49-55.
The music selection and the development and testing of the rules were
done as a team-work while all authors were present. All programming, development
of the listening test, analysis of the listening test and the writing of
a first draft was done by Anders Friberg.
Paper III.
Friberg, A., Sundberg, J. & Frydén, L. (1994). Recent musical performance research at KTH. in J. Sundberg (ed.), Proceedings of the Aarhus symposium on Generative grammars for music performance1994 7-12.
The development of the rules was done by Lars Frydén and Anders
Friberg. All programming, the listening test and the writing of a first
draft was done by Anders Friberg.
Paper IV.
Friberg, A., & Sundberg, J. (forthcoming). Time discrimination in a monotonic, isochronous sequence. J. Acoust. Soc. Am.
All programming, analysis of the listening test and the writing of a
first draft was done by Anders Friberg. The test was run by Johan Sundberg
and Anders Friberg.
Paper V.
Sundberg, J., Friberg, A. & Frydén, L. (1991). Threshold and preference Quantities of Rules for Music Performance. Music Perception 9 (1), 71-92.
The design of the tests were done by all authors. The programming was
done by Anders Friberg. The test was run by Johan Sundberg and Anders Friberg.
The threshold test was analysed by Johan Sundberg and the preference test
by Anders Friberg. Johan Sundberg wrote the paper.
Paper VI.
Friberg, A., & Sundberg, J. (1994). Just Noticable Difference in duration, pitch and sound level in a musical context. in I. Deliège (ed.), Proceedings of 3rd International Conference for Music Perception and Cognition, Liège 1994, 339-340.
The design of the listening test was done as a team-work by all authors.
All programming, analysis of the listening test and the writing of a first
draft was done by Anders Friberg. The test was run by Johan Sundberg and
Anders Friberg.
Paper VII.
Sundberg, J., Friberg, A. & Frydén, L. (1992). Music and locomotion. A study of the perception of tones with level envelopes replicating force patterns of walking. Speech Transmission Laboratory Quarterly Progress and Status Report, 4/1992, 109-122.
The measurement of the forces in the foot was done by all authors. The
translation of the force patterns to sound and the listening tests were
done by Anders Friberg. The analysis was done by Johan Sundberg and Anders
Friberg. The first draft was written by Johan Sundberg.
CD-ROM
Friberg, A., Sundberg, J. & Frydén, L. (1994). "Director Musices Demo 1.2" and "Music Examples", in Section The Art of Playing, in Information Technology and Music, CD-ROM, produced by the Royal Swedish Academy of Engineering Science.
"Director Musices Demo 1.2" was written by Anders Friberg.
The text in "Music Examples" was written by Johan Sundberg. The
rule examples in "Music Examples" were developed by Lars Frydén
and Anders Friberg.
Back to the Music Acoustics group Home Page