[<- Previous] [Contents of this lecture] [Next ->]
The mathematical treatment of the coupled motion of two strings which are tuned almost, but not exactly, alike is rather complicated, since the symmetry arguments which implicitly led to the identification of the "symmetric" and "antisymmetric" motions as normal modes of vibration no longer work. We shall, nonetheless, try to give some idea of the behavior of this complex system, but before we begin one thing must be made very clear, and that is that the presence of "mistuning" does not necessarily lead to beats, if by "mistuning" we mean a difference between the vibration frequencies of the two strings when they are individually excited (that is, when one string is made to sound with the other one damped). The point is, of course, that the frequencies of the two strings vibrating at the same time are affected by the coupling which occurs between them due to the bridge not being perfectly rigid.
A different, and perhaps clearer, way of explaining the distinction between the frequency of an isolated string and the frequency at which it vibrates when coupled, is to note first that the frequency of vibration of a string whose end-support is not completely rigid depends on the type of resiliency the string meets at the support, or using the scientific term, the impedance of the support, see Fig. 7. If the support is "springy," that is, one which displaces sideways in the direction in which the string applies a force to it, there will no longer be an exact node at the support. Instead, the extrapolated node will be somewhat beyond the physical end of the string; or, in other words, the string will "think" that it is longer than it really is, causing it to lower its frequency.
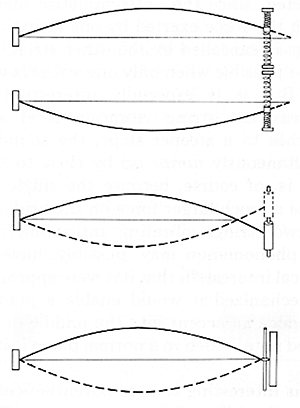Fig. 7 Illustration of the influence of the end-supports on the vibration frequency of a string. A "springy" support (top) lowers the frequency without damping the motion, because it makes the string act as if it was a little bit longer than it really is. A "massy" support (middle) raises the frequency without damping its motion. The reason is that the string must pull back on the mass to reverse its direction, the result being that the string acts as if it was a little bit shorter than it really is. A resistive support (bottom) does not influence the vibration frequency but damps the motion. The friction at the sliding contact at the support means that energy is drained from the string and the vibrations decay.
The opposite happens with a "massy" support, that is, a support whose motion is inertia-limited: in this case, its acceleration is in the direction of the applied force, and its displacement in the opposite direction. The node then moves inward from the physical end of the string, with the result that the string "thinks" that it is shorter than it really is so that its frequency is raised. Finally, if the support is purely "resistive," so that its velocity is in the direction of the force, its frequency is neither raised nor lowered, but its decay rate is increased.
If now a second string is attached to the bridge at the same (or almost the same) location, its presence will affect the impedance of the bridge as seen by the first string. The result is that the "frequency of the first string" will be different from its vibration frequency before the other string was introduced. How large this shift will be depends on the difference between the new "frequency of the first string" and its original frequency. We put the phrase "frequency of the first string" in quotation marks because it is really no longer that, but rather it is the frequency of the coupled normal mode in which both strings are vibrating.
To get some notion of how these coupled frequencies are affected by "mistuning" the strings, we should think about another impedance - not the impedance presented to the string by the bridge, but rather the impedance presented to the bridge by the other string. A simple demonstration experiment will illustrate this behavior. If I attach a rope (representing the string) to a fixed chair and shake the other end up and down at some arbitrary frequency of my choosing, the fact that I am holding the end of a rope will make very little difference to what I feel. But if the frequency I choose corresponds to one of the resonant frequencies of the string, the place where I hold it becomes a node and "refuses to move." It is as though the fixed point at the other end of the string were transferred to the holding point; even though I am exerting a considerable force amplitude up and down, my hand almost does not move at all. Paraphrasing this behavior in terms of impedance, we would say that the impedance presented by the string to its support is generally quite low, but becomes very high as the frequency approaches a resonant frequency of the string.
It should be clear from this discussion that if we observe the motion of two coupled strings, of which one is left untouched while the other is tuned, we would observe that the untouched string will change its frequency (although it remains at constant tension) as the second string is tuned. This is under condition that the two strings are close to a unison, since under those circumstances the impedance of the second string at the frequency of the first string becomes quite high, modifying the effective impedance of the bridge as seen by the first string. What is not so clear - and, in fact, requires considerable mathematical discussion - is precisely what this frequency shift will be. Interestingly, it turns out that it can be in either direction, depending on the impedance of the bridge itself. In particular, there exists a possibility for the two frequencies to "attract" and become locked together, so that slight tuning of either string does not affect the frequency of either but only the decay rates. This is what we meant by saying that a slight "mistuning" of the strings does not necessarily lead to the appearance of beats.
The last figure, Fig. 8, shows some theoretical curves of the history of the vertical force exerted on the soundboard when driven by two strings, initially excited by a perfectly symmetric hammer blow. The different curves correspond to different "mistunings," and the bridge impedance is assumed such as to allow the "locking together" of the frequencies (which is not always the case in practice). In calculating these curves, we have assumed parameters more or less typical of the middle range of a piano keyboard. For this case, there are no beats unless the "mistuning" is more than about 0.3 Hz; more correctly, for smaller "mistunings" there is just a single "beat null," followed by a beatless aftersound whose level depends on the "mistuning." Above about 0.3 Hz beats do appear, as exemplified by the curve drawn for a "mistuning" of 0.64 Hz; even here, however, the time between beats is a bit larger than the 1.6 seconds which would be naively predicted (1/0.64 Hz = 1.6 s). The importance of Fig. 8 is that it indicates how an excellent tuner can, under some circumstances, use very fine tuning control in order to adjust the aftersound of each note to a more uniform level than if it were due entirely to imperfections in the hammer or the string mountings.
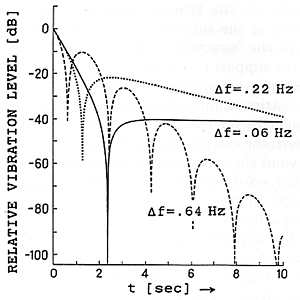Fig. 8 Calculated vertical force on the soundboard when driven by two strings with different "mistuning" ( f). In this example beats occur only when the "mistuning" is larger than 0.3 Hz, illustrated by the curve for f = 0.64 Hz. For smaller values the strings lock to a common frequency, and the effect of the "mistuning" is to control the level of the aftersound (cf. the curves for f = 0.22 Hz and 0.06 Hz).
In fact, it was observed by Kirk in 1959 that a carefully and competently tuned piano had the strings of the trichords tuned slightly differently by an amount that appeared to vary randomly from note to note. This randomness may, however, hide an underlying regularity. If, for example, you take a sheet of paper and tear it, examination of one of the pieces will reveal an irregular and seemingly random rough edge; yet comparison with the other piece will show that one irregularity exactly matches the other. Our hypothesis here is that, in the same way, the seeming "randomness" of the tuning comes from the fact that the skilful tuner was adjusting this quantity to another randomness, namely the randomness of hammer imperfections, in such a way that the result is not random. It would be interesting to test this hypothesis by investigating, for example, whether good tuners are consistent in the "mistuning" of the individual trichords when tuning the same piano over and over again.
[<- Previous] [Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music