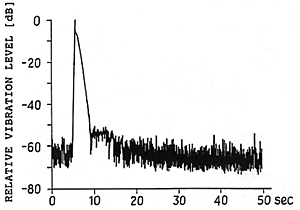
 Fig. 3 Typical decay of the vertical string vibrations when only one string in a trichord is left free to vibrate.
Fig. 3 Typical decay of the vertical string vibrations when only one string in a trichord is left free to vibrate.

[<- Previous] [Contents of this lecture] [Next ->]
The more interesting mechanism which leads to an aftersound - and which, as we shall see, makes it possible to adjust its relative amount by careful tuning - is the one on which the title of this lecture is based, namely the dynamical coupling among the three (or two) strings struck by the same hammer. Let us imagine two identical (and identically tuned) strings attached to the bridge at the same place. It is possible for them to vibrate in the same phase, both going up and down at the same time; or in opposite phase, one going up while the other is going down. (In the present discussion we concentrate, for simplicity, on the vertical motion.) In the latter, "antisymmetric," case the forces exerted by the two strings on the bridge will cancel, so the bridge will not move at all, just as though it were infinitely rigid. Hence, the decay rate of the vibration will be very slow. Conversely, if the motion is in phase, or "symmetric," the force on the bridge (and hence its displacement) will be twice as large as it would be for one string, so the decay rate will be doubled by this coupling. In this way we see the possibility for the overall vibration to decompose into a prompt sound and an aftersound.
The experimental data of Figs. 3 and 4 illustrate this behavior. The graph in Fig. 3 shows the vibration level of a single string; it differs from our previous graphs in that this time the motion of the string is directly measured (by a capacitive probe designed to be sensitive only to the vertical motion), rather than recording the radiated sound via a microphone. As in Fig. 1, felt wedges prevent all but one string from vibrating. The general behavior is equivalent to the prompt sound part of Fig. 1, except that the time scale of the graph has been considerably expanded.
 Fig. 3 Typical decay of the vertical string vibrations when only one string in a trichord is left free to vibrate.
Fig. 3 Typical decay of the vertical string vibrations when only one string in a trichord is left free to vibrate.
The graph in Fig. 4 is obtained in exactly the same way, except that one felt wedge is removed so that one other string of the trichord is allowed to vibrate. It must be emphasized that the capacitive vibration probe is not disturbed; what we are looking at is the vertical motion of the same string as before, except that a second string has been "brought into the system." Clearly, a new mode of vibration has now appeared, one in which the original string can vibrate for a much longer time before it loses its energy. It is, in fact, precisely the antisymmetric mode which is allowing this to happen.
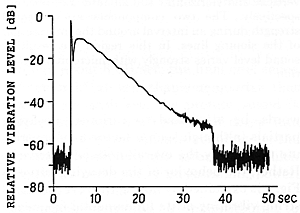 Fig. 4 The decay pattern of the same string as in Fig. 3 when another string in the same trichord is left free to vibrate (but not struck by the hammer). The decay of the first string is strongly influenced by the motion of the other string.
Fig. 4 The decay pattern of the same string as in Fig. 3 when another string in the same trichord is left free to vibrate (but not struck by the hammer). The decay of the first string is strongly influenced by the motion of the other string.
A closely related phenomenon is illustrated in Figs. 5 and 6. The curves in Fig. 5 show both the vibration level of one of the strings and the (simultaneous) sound level, produced when two strings are struck by a single hammer under circumstances similar to Fig. 4. In Fig. 6 the experiment is repeated, but at about t = 11 seconds a felt wedge is suddenly inserted so as to immobilize the second string. We see that the vibration of the first string, as well as the produced sound, change immediately to the higher decay rate. This is, indeed, expected, since the antisymmetric mode (in which the force exerted by one string on the bridge is cancelled by the other string) is no longer possible when only one string is vibrating. But it is especially interesting that, whereas the string vibration level simply switches to a steeper slope, the sound level simultaneously jumps up by close to 20 dB. This is, of course, because the single string exerts a much larger force on the bridge than the two strings vibrating antisymmetrically. The phenomenon may, possibly, have some musical interest, in that if it were appropriately mechanized it would enable a pianist to introduce an accent into the middle of a sustained note, which in a normal piano is impossible.
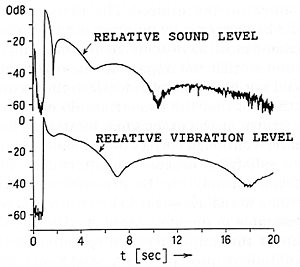 Fig. 5 Sound pressure level and string vibration level versus time for two strings struck by the same hammer. The humps reflect beats between the strings.
Fig. 5 Sound pressure level and string vibration level versus time for two strings struck by the same hammer. The humps reflect beats between the strings.
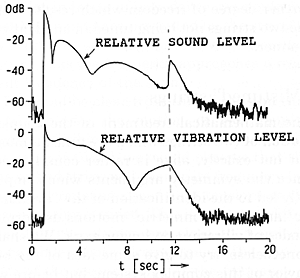 Fig. 6 The same curves as in Fig. 5 but now the vibrations of one of the strings is stopped at t = 12 s by a felt wedge. This terminates the interaction between the strings, as a result of which the vibrations of the other string change decay rate and the sound level momentarily increases by 20 dB.
Fig. 6 The same curves as in Fig. 5 but now the vibrations of one of the strings is stopped at t = 12 s by a felt wedge. This terminates the interaction between the strings, as a result of which the vibrations of the other string change decay rate and the sound level momentarily increases by 20 dB.
It is interesting to note parenthetically the rather complicated beat structure in Figs. 5 and 6, which is not precisely the same for the vibration and the sound. Presumably, the discrepancy comes from the horizontal modes, which contribute to the sound but not to the vertical motion.
Two questions immediately arise: (a) If the hammer hits both strings equally and at the same moment, why is the motion not completely symmetric, resulting in "purely prompt" sound? (b) Even if the antisymmetric vibration is somehow excited, why does it produce any sound at all, seeing that it exerts no force on the bridge? The first question could be answered by pointing out that a real hammer must have some geometrical imperfection so that the impact on the two strings would not be absolutely identical; the second, by the fact that the two strings do not touch the bridge at the exact same location. These answers, although correct in principle, are not very satisfying because an aftersound that depends entirely on the presence of imperfections would also tend to be erratic and unpredictable in amount. More specifically, the ratio of the amplitude of aftersound to the amplitude of prompt sound would vary randomly when one note is compared with its neighbouring ones. This would give even a very good piano a rather uneven "singing quality." In fact, the correct understanding of the string motion requires us to consider the further degree of freedom which results from the two strings not being tuned in an identical manner.
[<- Previous] [Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music