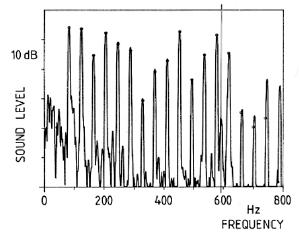
 Fig. 32. Spectrum of piano note E1 (41 Hz) showing longitudinal mode (indicated by the vertical line at about 600 Hz).
Fig. 32. Spectrum of piano note E1 (41 Hz) showing longitudinal mode (indicated by the vertical line at about 600 Hz).

[<- Previous] [Contents of this lecture] [Next ->]
Of course there is more to designing good piano scales than merely calculating the tension of the strings. In 1967, I applied for a patent under the heading, "Longitudinal Mode Tuning of Stringed Instruments" (Conklin 1970). I found the technique outlined in this patent to be such a powerful tool in scale design work, especially in the design of wrapped strings, that today I would not consider designing a piano without it.
In longitudinal modes of vibration, energy propagates lengthwise along the string (as periodic compressions of the string material) without sidewise (transverse) motion of the string. Longitudinal and transverse vibrations of a piano string can occur simultaneously. However, the lowest-frequency longitudinal mode of a piano string is always more than ten times the frequency of the lowest-frequency transverse mode.
It has long been known that the strings of pianos and other musical instruments can have longitudinal modes of vibration (Rayleigh 1877, Knoblaugh 1944, Leipp 1969). My patent simply teaches what the designer should do about it in order to make the best sounding instrument. I learned the importance of the longitudinal mode by accident; one day, while I was installing a new string, I noticed that the string sounded better when it was tuned to the wrong frequency! After some study it became apparent that the reason had to do with the longitudinal mode. The first longitudinal mode of a piano string normally occurs at a frequency somewhere in the range between 3 octaves plus a fifth and 4 octaves plus a third above the "normal" fundamental transverse frequency of a string. This range is determined by certain design constraints related to the properties of piano wire that are common to all present-day pianos.
A piano tuner tunes the transverse, or flexural, modes of the strings by changing the tension of the strings as he turns the tuning pins. A piano tuner can do nothing to affect the frequency of the longitudinal mode because turning the tuning pins doesn't change it. The longitudinal frequency of a plain steel string in a piano can be changed only by altering its speaking length. In the case of wrapped piano strings, the longitudinal mode can be tuned only in two ways: either by changing the speaking length or by changing the weight of the wrapping wire in relation to the weight of the core wire. So, the tuning of the longitudinal mode is established, either deliberately or accidentally, by the designer of the piano; and, as a practical matter, it cannot be changed after the piano has been built.
In designing a piano nowadays, it is possible to tune the longitudinal modes of its strings to those frequencies that will make the piano sound best. In sound example 4, you can hear what kinds of changes in the timbre of piano tones are produced by changing the tuning of the longitudinal mode.
I think you will agree that each string sounds different from the others. However, all those six strings were tuned to the same transverse frequency by a piano tuner: all the notes were low G1 (key 11) on the piano! They sounded different because each had a different tuning of the longitudinal mode. In sound example 5, you can hear a little tune which is known as "Yankee Doodle". The tune is played in two different keys.
I am sure you will recognize that a tune is being played. However, the tune was played on strings that were all tuned to the same transverse frequency! The tunes could be heard because each string was designed so that its longitudinal mode differed in frequency by a semi-tone (100 cents) from that of the preceding string. (The common transverse frequency was not the same for the two versions in different keys.)
Next, listen to some chords, each chord followed by a bass note having a different tuning of the longitudinal mode but the same tuning of the transverse mode (sound example 6).
As I hope you can hear, the longitudinal mode is important in determining the tone color of the bass and tenor regions of the piano. The longitudinal mode creates a formant-like emphasis in the tone at its own frequency, with the result that some tunings of the longitudinal mode sound much better than others. In particular, it is desirable to have the longitudinal mode tuned so that it blends harmoniously with the tone from the transverse modes. This can be achieved by careful and deliberate choices in the design of the strings and scale of the instrument.
In the examples you have heard so far the longitudinal mode was deliberately tuned at intervals of a certain number of semi-tones with reference to the fundamental transverse mode. Strange and undesirable things can happen to the tone if the longitudinal mode is ignored or left to chance by the designer. Next you will hear some scales played on two different pianos. The first piano has the longitudinal mode tuned by design, the second one does not. As you can hear, the piano having deliberately tuned longitudinal modes has a much more uniform and pleasing voice through the scale (sound example 7).
Physicists may want to know if it is possible to measure what we are hearing. Fig. 32 is an acoustical spectrogram of piano note E1, with a fundamental frequency of about 41 Hz. The "normal" transverse partials are identified by small dots near each peak. The longitudinal mode can be seen between the 14th and 15th partials and is about 20 decibels lower in level than the neighboring partials (Podlesack & Lee 1988).
 Fig. 32. Spectrum of piano note E1 (41 Hz) showing longitudinal mode (indicated by the vertical line at about 600 Hz).
Fig. 32. Spectrum of piano note E1 (41 Hz) showing longitudinal mode (indicated by the vertical line at about 600 Hz).
Machines similar to those shown in Fig. 33 have been used for a long time to wind the copper covering wire onto wrapped piano strings. With these machines the characteristics of the finished strings are strongly dependent upon the technique of the operator. Operator technique varies, not only from person to person, but also from string to string. It was found to be impossible with such machines to control the tuning of the longitudinal mode precisely enough so that successive strings could be accurately tuned and alike in tone. For this reason, it was necessary to design a new type of machine, also patented, with which the characteristics of the finished string would be independent of the operator. With this machine, optimum settings are predetermined for each type of string.
 Fig. 33. Old string machines.
Fig. 33. Old string machines.
[<- Previous] [Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music