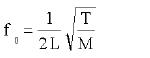

[<- Previous] [Contents of this lecture] [Next ->]
The fundamental frequency of a stretched string is given by the expression below, known since the beginning of the 17th century, in which L is the length of the string, T is its tension or pull, and M is its mass per unit length.
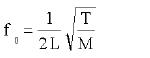
The fundamental frequencies of a modern piano are known in advance because A4 has a standard frequency (440 Hz) and because the frequencies of adjacent notes all across the equally tempered scale have a ratio equal to the twelfth root of 2, about 1.05946. The most common calculation in designing a piano scale is the tension, not the frequency of the string. (The scale is the distribution of the string lengths and gauges over the compass of the instrument). The above expression can easily be rearranged to give the tension. Also, a factor (F) can be added to the formula above to allow for the use of wrapped strings, and a changeable constant (k) may be employed in order to permit calculation for any string material in any system of units. Then the tension of a string may be written as:
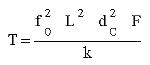
In this formula, dc is the string diameter (or the core wire diameter, in the case of a wrapped string). F is unity (1) for a plain string but has some larger positive value for a wrapped string. For a string of steel music wire for which the length and diameter are given in centimeters, the tension will be given in Newtons (N) for k = 4096. I show this formula to make a certain point: there's a lot of multiplying here! In the old days it could take a long time to calculate just one string. What if you had to do this for 88 different strings with only pencil and paper?
Much in early piano design obviously was empirical. Empiricism seems to have persisted for longer than one might expect. Would you believe that even in the 20th century, piano designers still didn't know how to calculate the tension of a wrapped string, and had to find it by actual measurement. (Wrapping the core of a string helically with turns of another wire is a very old method, still in use, to make a bass string heavy without having its core too thick and thereby too stiff to produce a good tone.) The following sentence appears in a supplement, dated 1927, to Wolfenden's well-known book about piano design:
"It is remarkable that, at this date, after spun strings have been in use for, say, a matter of two centuries, neither in this country nor any other, as far as many enquiries have shown, is there in trade use, a method by which the tensional stress upon a spun string, tuned to a given pitch, can be approximately ascertained" (Wolfenden 1927).
Equations for calculating the pull of wrapped piano strings are now well known to at least some piano manufacturers and also to many piano technicians. Also, with computers we can calculate piano strings and scales very accurately and much more quickly than ever before.
[<- Previous] [Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music