[<- Previous] [Contents of this lecture] [Next ->]
We should not trust those calculations too much without making some measurements on real pianos. I had the opportunity to make such measurements together with Anders Askenfelt in 1985 at the Royal Institute of Technology in Stockholm (which is reported in more detail in Hall & Askenfelt, 1988). One of the things we did (Fig. 13) was to measure the string motion on a 2 meter Grotrian-Steinweg piano. For this we placed a small magnet so that the string would move between its poles; this motion generated an electrical voltage which we could record and analyze.
Fig. 13. Placement of detectors for measuring string velocity and hammer acceleration.
In sample results for middle C (Fig. 14), we can observe a repeated pattern of string motion when it is vibrating freely. But during the time the hammer is in contact with the string, we see evidence of the action of individual reflected waves travelling between the hammer and the agraffe. (The upper oscilloscope trace tells directly about the force acting between hammer and string.)
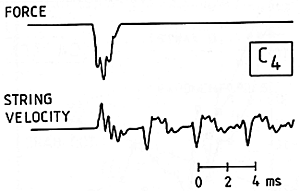Fig. 14. Oscilloscope traces of hammer acceleration (top), which is proportional to force, and of string velocity (bottom) for middle C played mezzo forte.
A spectrum analysis of this data shows (Fig. 15) rapidly declining strength for higher mode numbers. If we compare a 12 dB/oct curve, we can see that the measured spectra are much steeper, especially for pianissimo playing, so that our simple "first guess" (cf. Fig. 3) is not nearly good enough in explaining what happens. Another interesting result came when we measured a prepared set of hammers with different degrees of "pricking" (voicing) of the felt (Fig. 16).
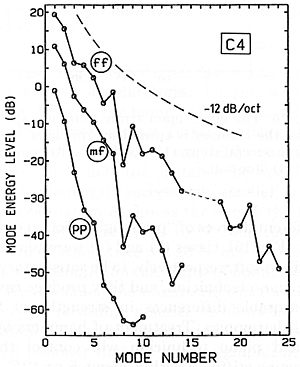Fig. 15. Measured string vibration spectra for middle C, struck with different degrees of force.
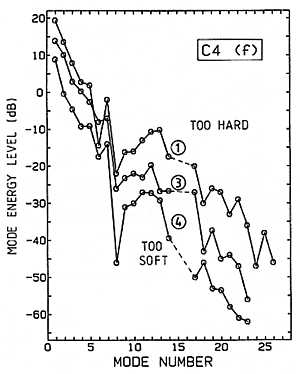Fig. 16. The effect upon string vibration spectra when the hammer is treated by "pricking" (voicing); (1) "too hard", (3) "normal", and (4) "too soft."
Cases (1) and (4) were too hard and too soft, respectively, to be satisfactory to the piano technician, and they produce easily measurable differences in strengths of the high harmonics. Treatment of hammers by a skilled piano technician will control their effective stiffness within about 5 or 10%, or even less.
Now we must compare such measurements with predictions made by the computer (Fig. 17). We find that there is resemblance in some of the general features of the spectra, but definitely not good agreement in detail, no matter which value of hammer stiffness we try. To see what is probably the most important reason for this, look back again at Fig. 15, and notice that the pianissimo spectrum is much steeper than the fortissimo. This means, as all musicians realize, that the sound of fortissimo playing is not the same as if you merely play pianissimo and use an electronic amplifier. The first case is not merely louder, it has a brighter tone quality as well.
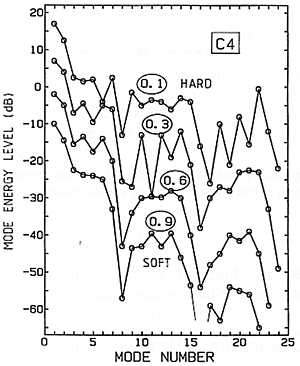Fig. 17. Predictions from linear theory, to be compared with Figs. 15 and 16. Compliance varies from 0.1 (hard) to 0.9 (soft).
But the theory I have described so far is a "linear" theory. This means one in which a doubling of the original hammer velocity would simply double the amplitude of string motion, double the soundboard motion, and double the air motion at your eardrum, without changing any other detail. That is, it predicts the same spectrum shape for both piano and forte playing; a single curve shifted upward and downward would cover every case. This is clearly wrong, and it will be important for us to identify which part of the system has "nonlinear" properties, and devise some way of including that in a better theory.
I believe the crucial part of the system lies in the hammers. In order to show this, Askenfelt and I made some measurements of how the hammers from the Steinweg piano act in a controlled situation outside the piano. We mounted a force measuring device in the chuck of a drill press, and placed the entire keybed below it. Then when we hit the keys in the normal way, any hammer could be thrown against what is effectively a solid wall instead of against yielding strings. We recorded how the force on the hammer changed during the brief contact by using a storage oscilloscope, with results like those in Fig. 18. Now if the hammer were an ideal "linear" device, those two curves would be equally wide. This phenomenon would be like the swinging of a pendulum, which for a given length takes the same amount of time whether it swings ten degrees or only one degree. But contact time was actually much shorter for the stronger blow; therefore the hammer felt acts as a non-ideal, nonlinear spring. To get an idea of how such a spring works, one can think of a helical spring in which the distance between the turns (pitch) gets successively smaller. If the force needed to compress the spring the first centimeter is, let's say, 10 N, then the next centimeter may take not 20 N, but 40 or even 80 N, depending on the degree of nonlinearity.
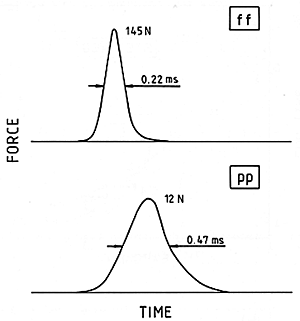Fig. 18. Force histories when a real piano hammer hits a rigid wall. The vertical scale is expanded for the soft blow (pp), during which the maximum force was less than 1/10 as much as for the hard blow (ff).
We examined the nonlinearity in the hammers by recording a series of blows for two hammers in each octave, producing data for each hammer that we analyze graphically as shown in Fig. 19. Here the lines would be horizontal if the hammer were a linear device; the greater the slopes of these lines, the greater degree of nonlinearity, and therefore the greater difference in the way the hammer will act between pianissimo and fortissimo playing.
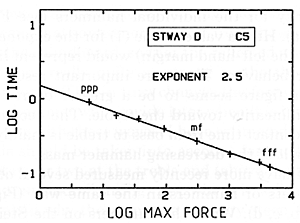Fig. 19. Decrease in contact time with increasing strength of blow, graphed so that greater slope indicates greater degree of nonlinearity in hammer stiffness.
To see whether there is any definite trend in the hammer properties from bass to treble, we use the slopes from the graphs to compute a value (exponent) telling the degree of nonlinearity for the individual hammers (see Fig. 20a). Here a value of one (1) for the exponent (at the left-hand margin) would represent linear behavior. The more important result in this figure seems to be a greater degree of nonlinearity toward the treble. The decrease in contact time from bass to treble is mainly a result of the decreasing hammer mass.
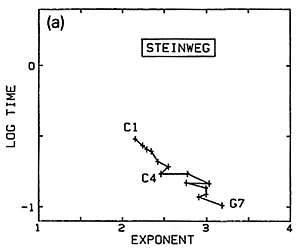
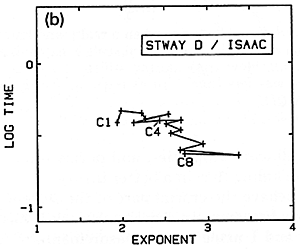
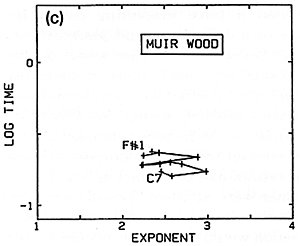
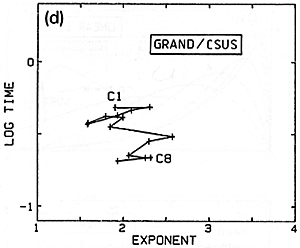
Fig. 20 a,b,c,d. Variation of nonlinearity exponent from bass to treble for several different sets of hammers.
I have more recently measured several other sets of hammers in the same way (Figs. 20b,c,d). While the hammers on the Steinweg piano had been in use for some time, the Isaac hammers were a brand-new set just being installed on the large Steinway D in my university's Music Recital Hall, and were not yet "played-in". The Muir Wood is a Scottish piano from around 1800 - 1810, restored and located in the Department of Music at the University of California in Berkeley. There is perhaps less difference between treble and bass here, but from the variations one suspects that the hammers are presently not in very good, uniformly-voiced condition. A grand in the piano technician's workshop at my university (CSUS) was chosen as an example of an instrument with a very worn set of hammers in poor condition, producing a harsh, unpleasant sound (Fig. 20d).
I do not yet feel sure that I know how to interpret these differences from one set of hammers to another. If I had guessed before measuring, I would have thought the harsher sound of the bad hammers might mean a larger value of the nonlinearity exponent, but according to the measurements it is really smaller instead. I can explain this if, when we said harsh or unpleasant, what we really meant was specifically that we did not get as much darker tone as we expected when trying to play softly. Askenfelt has suggested that this may be partly because well-used hammers develop flat grooves that cannot make as gentle a contact as the original rounded shape. Before stating any firm conclusions, I would want to make this kind of measurements on many more sets of hammers, from different makers and in different conditions.
[<- Previous] [Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music