Back to Contents of Five lectures...
[Contents of this lecture] [Next ->]
If we want to have a full understanding of how the best piano music is heard, we have many things to consider, as I have outlined in Fig. 1. Many important and complicated things happen in our fingers, ears, and brains; I can recommend a recent book for some enjoyable reading about those things (Wilson 1986). Even the physical processes through which the piano generates sound (the motions of the hammer, strings, and the soundboard) involve several stages which all require careful work to understand. I want to start by supposing that the hammer is already moving in the proper way, and studying how it gives its energy to the string. If we could understand that striking process completely, then we could know what kind of string vibration reaches the bridge and serves as input for the more difficult question of how the soundboard works.
Fig. 1. Steps in the process of playing the piano.
We can see better what kind of problem we have by comparing some other instruments. When we pluck a guitar, harp, or harpsichord, the process is well described by saying that the string is first held steadily in a triangular shape; at the moment of release, the finger or plectrum "suddenly" disappears and leaves the string to vibrate freely. This motion of the string by itself is a simple enough physical problem that we can summarize it in Fig. 2. When we show the spectrum, which tells the strength of each harmonic component in the string vibrations, the triangular initial shape of the string always provides an envelope curve requiring that the vibration level decreases by 6 dB (meaning 1/4 as much energy) for every octave higher in frequency. The particular place where the plucking was done acts further to suppress any harmonics which have nodes at that point; for example, plucking a 50 cm long string 10 cm from one end gives a spectrum in which the fifth, tenth, and fifteenth etc harmonics are absent.
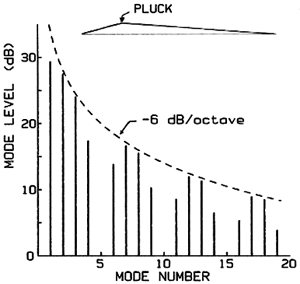Fig. 2. Theoretical spectrum of vibration mode energies for a string plucked one-fifth of its length from one end.
If we try to think of a similar simple picture for a piano string, we might consider two possibilities. First, imagine that the hammer pushes the string into a triangular shape, as for the harpsichord; then the string must push the hammer back down in a similar way as an arrow is moved by a bow-string (Fig. 3). If that motion is slow enough that the string always has the shape of a triangle, merely getting more and more shallow, we can predict a harmonic spectrum much like that for plucking. The only difference is that it falls off at a faster rate, 12 dB per octave. Unfortunately, this prediction is very different from what we measure in real pianos. That is not surprising when we say that we should not expect that picture to be correct unless the hammer is much heavier than the string, which is true only for the extreme treble end of a piano.
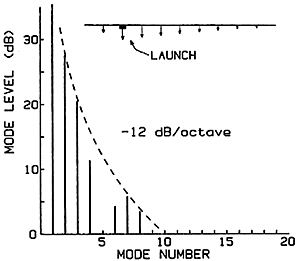Fig. 3. Naive prediction of possible vibration spectrum for a thin string struck by a very massive hammer.
A second simple picture would be that the hammer bounces away so quickly that most of the string does not even begin to move while the hammer is touching. This picture leads again to an incorrect prediction, namely that the harmonic strengths do not fall off at all toward higher frequencies (0 dB/oct), apart from the "holes" related to the striking position (Fig. 4). Again, we realize that we should not expect this picture to be correct unless the hammer is much lighter than the string, as in the extreme bass range - and yet, even there, the predictions do not agree well with measurements. You will notice that these two incorrect pictures are quite contradictory as to whether the piano's sound would have a brighter or a darker spectrum (0 dB/oct or -12 dB/oct) than a harpsichord (-6 dB/oct).
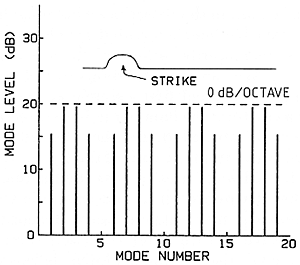Fig. 4. Naive prediction of possible vibration spectrum for a string struck a very brief blow by a hammer with very little mass.
We see that we can only come to a correct understanding by admitting that the hammer remains in contact with the string for a finite time, during which the force exerted by the hammer upon the string may change in a complex way. In Fig. 5 we are reminded of how the effective hammer mass may vary only from about 12 g in the bass to 6 g in the treble, while the string masses cover a much wider range. (Note that where there is double or triple stringing, it is the total string mass for each note that is important here.) Since the hammer mass makes it about an equal partner with the string through much of the important middle range of the piano, we are not surprised to see in Fig. 6 that measured contact times in the middle range are quite similar to half of the period with which the string would vibrate alone - and longer than the vibration periods of most of the upper harmonics.
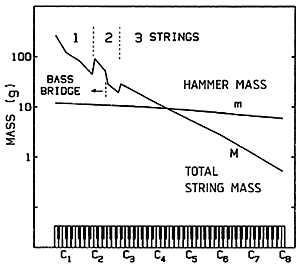Fig. 5. Comparison of hammer mass (m) with total string mass (M) on a typical grand piano.
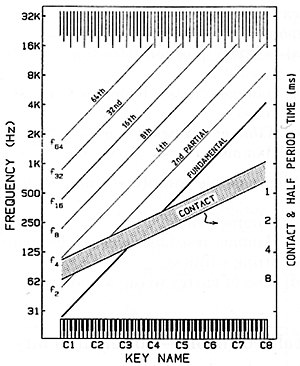Fig. 6. Comparison of string mode frequencies with typical hammer contact durations.
So if we want to understand what is happening during this process we must be able to measure the string and hammer motion on time scales shorter than a millisecond. And, to construct a correct theory explaining this process, we must study how the hammer and string each control what the other is doing during that very brief time of contact. Appropriate things to try to understand would include:
Duration of hammer-string contact - how long?
Energy transfer to the string - how efficient?
String motion after contact ends - what spectrum?
Parameters - How do each of those depend upon:
Other possible complications (less important):
[Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music