[<- Previous] [Contents of this lecture] [Next ->]
What else can we do that may give us a more firm understanding of the interaction of the string and hammer, and of how to shape that interaction to produce whatever spectra we find most useful musically? As for theory, there is a first step that is not very difficult. That is to calculate the wave shape, or the corresponding force (Fig. 22), for the very first wave that travels away from the hammer. The upper panel shows the case of a linear hammer, already treated in great detail in our earlier theory, with the curves peaking sooner for harder hammers and more gradually for softer ones. The lower panel shows how these force histories would change in the presence of a certain fairly large degree of nonlinearity. Perhaps there is a suggestion in these curves that the nonlinearity tends to increase their similarity, making them less dependent upon our ability to control the stiffness (K) exactly.
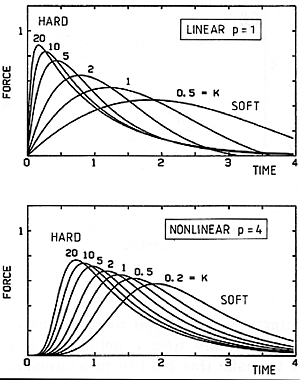Fig. 22. Force histories (initial wave only) for linear hammers, exponent p=1 (upper panel) and nonlinear hammers with exponent p=4 (lower panel). In each case, larger values of K denote harder hammers. Normalized plot, the same "units" as in Fig. 11.
Unfortunately, those pictures only tell us how the hammer interacts with an infinitely long string. We cannot go on to include reflected waves by simply adding several of these together; some entirely different mathematical method must be introduced to solve the nonlinear equations of motion. Some sample calculations of this sort have recently been done by Suzuki and by Boutillon. Fig. 23, which is from Suzuki (1987), shows one calculated case of a bass hammer interacting with the A0 string of a 6-foot Steinway grand. Curve (a) shows the hammer position and curve (b) the string displacement at the contact point; we may notice that where (b) rises above (a) the hammer loses contact, but there is renewed contact when the reflected wave arrives from the agraffe. Curve (c) gives the force experienced by the string, from which the vibration spectrum can be obtained. Fig. 24, taken from Boutillon (1988), shows a calculated case for one particular hammer hitting F4; the dashed line gives the calculated history of hammer acceleration, and the solid line is a corresponding measurement.
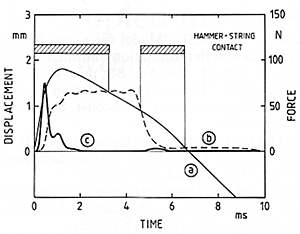Fig. 23. Time histories of (a) hammer displacement, (b) string displacement, and (c) interaction force for a bass hammer (A0) with nonlinear compliance (Suzuki 1987).
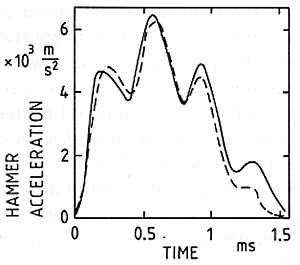Fig. 24. Comparison of predicted (dashed) and measured (solid) accelerations for a nonlinear hammer (F4), (Boutillon 1988).
But we do not yet have a wide range of such cases computed in order to see how the results change if we alter the important parameters such as hammer mass, stiffness, striking point, and degree of nonlinearity. Nor can we yet compare the predictions with actual measurements for a wide range of notes and of different pianos. I have some students interested in working on this problem, and I entertain some hopes that we may write a new computer program that will make it possible to explore the action of nonlinear hammers in a systematic way. Perhaps it is not very far in the future that we may be able to claim the ability both to understand and to predict with some accuracy just what changes in sound will result when string and hammer designs are changed in various ways. We could hope that this would eventually contribute to useful diagnosis of what could be expected from any proposed change in hammer design or manufacturing technique.
In the meantime, I could see the possibility of one practical application of this work in the manufacture of new piano hammers. Good quality control on a new set of hammers means both that we achieve desired values of hardness and nonlinearity, and that these properties change smoothly as we go along the row of hammers. Either before or after work by the voicing technician, this could be checked by placing the keybed in a frame where it would be moved in 88 steps. At each step a mechanical striker would hit the key, perhaps 5 or 6 times, ranging from very weak to very strong impulses. The hammer would hit a force transducer, and a computer would evaluate the height and width of the signal produced. With this data, the computer could estimate the effective stiffness and nonlinearity of each hammer head, and produce either graphs showing how these properties vary from treble to bass, or lists with warnings of which hammers are not in good agreement with their neighbors. One could perhaps also devise a quick-clamp rig so that a set of hammer heads could be tested in this way without being mounted on shanks in an action. I hasten to add that this test should only be an aid to the technician, and would never entirely replace the voicer's ear as the final judge of good hammer preparation.
[<- Previous] [Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music