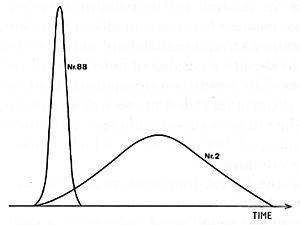
 Fig. 1. Force pulses of the hammer impacts for a bass note (No: 2 = Bb0) and a treble note (No: 88 = C8).
Fig. 1. Force pulses of the hammer impacts for a bass note (No: 2 = Bb0) and a treble note (No: 88 = C8).

Back to Contents of Five lectures...
[Contents of this lecture] [Next ->]
When a piano key is depressed, the hammer is accelerated from its rest position via a series of levers, called the "action," and catapulted against the string. Shortly before the string impact, the direct contact between the action and the hammer is interrupted, and the hammer is carried the rest of the way to the string by its momentum.
The shape and amplitude of the force pulse generated at the impact is determined by the final hammer velocity and by a combination of the mechanical properties of the hammer head and the strings (mass ratio, striking position, and stiffness of the hammer). The hammers and strings are designed so as to make the force pulse shorter in the treble than in the bass (see Fig. 1).
Such a pulse corresponds to a spectrum, which spans a broad frequency range (up to 10 kHz for a treble hammer). From this continuous pulse spectrum, the string filters out the frequency components corresponding to its resonant frequencies. These string spectrum components transfer the vibration energy to the bridge. Both the properties of the string material and the dimensions of the string influence this energy transfer.
 Fig. 1. Force pulses of the hammer impacts for a bass note (No: 2 = Bb0) and a treble note (No: 88 = C8).
Fig. 1. Force pulses of the hammer impacts for a bass note (No: 2 = Bb0) and a treble note (No: 88 = C8).
The bridge serves as the connecting element between the string and the soundboard, transferring the vibrations of the string into the soundboard. The strings are distributed over the entire length of the bridge which extends approximately diagonally across the soundboard. As a consequence the strings will deliver their vibration energy at different points on the soundboard, which means that they will all encounter different matching conditions.
The soundboard transforms the mechanical vibrations into radiated sound. As a first approximation, the soundboard acts like a large diaphragm clamped around its edge. Like all diaphragms, the soundboard exhibits a series of resonances, the individual intensities being determined by the point of excitation.
If we ignore the resonances for a moment, a diaphragm exhibits a radiation efficiency that increases as a function of frequency and reaches a theoretical maximum in the upper treble region. This would mean an optimal match between the soundboard and the surrounding medium in the upper treble, provided no losses occurred in the wood. Losses do occur, however, and these result in a decrease in the sound radiation in the upper treble.
With increasing frequency, the dimensions of the soundboard also become increasingly large in relation to the bending wavelength. This means that the soundboard no longer vibrates as a simple stiff diaphragm, but tends to divide into a number of individual vibrating areas. The result is a pronounced peaking of the directional radiation, as well as a decrease in the radiated acoustic energy - air is uselessly pumped between areas which vibrate in opposite phases.
In the lowest frequency region, the lack of separation between the upper and lower surface of the soundboard reduces the sound radiation (acoustic short-circuiting).
Altogether these phenomena result in a favored region of acoustic radiation at frequencies between approximately 100 Hz and 2000 Hz.
Returning to the soundboard resonances, we note that it is particularly easy to vibrate the soundboard at the resonant frequencies. Using a constant driving force, we therefore obtain a high vibration amplitude and velocity at these frequencies. The quotient of force and velocity gives us a highly informative quantity called mechanical impedance, which can be easily measured as a function of frequency (see box below). The resonance frequencies of the soundboard are readily observed in such an impedance curve, where we find them at the valleys, or minimum values. The contribution to the sound radiation from each resonance must, however, be determined from another measurement, that is, sound level versus frequency. This quantity is also readily measured.
In addition, by means of a modern technique called modal analysis, the vibration pattern of the soundboard at the resonances can be computed from simple measurements and visualized on a terminal screen. This technique also allows computer simulations of changes in the shape and thickness of the soundboard, which thus can be evaluated before a new prototype instrument is built.
[Top] [Contents of this lecture] [Next ->]
This lecture is one of Five lectures on the Acoustics of the piano
© 1990 Royal Swedish Academy of Music